UNIT 6 ΟΡΙΖΟΝΤΙΑ ΒΟΛΗ

ΟΡΙΖΟΝΤΙΑ ΒΟΛΗ

Έστω σώμα μάζας m ,εκτοξεύεται με οριζόντια  ταχύτητα υx=υ0 από ύψος Η.
Η κίνηση αυτή που εξελίσσεται με την επίδραση μόνο του βάρους ονομάζεται οριζόντια βολή.(θεωρούμε ότι δεν υπάρχουν τριβές και άλλες δυνάμεις εκτός του βάρους) 
Παρακολουθήστε στο παρακάτω video την κατάβαση ενός σκιέρ.

ΚΑΤΑΒΑΣΗ ΣΚΙΕΡ

Ο σκιέρ τη στιγμή της εκτόξευσης του ,έχει οριζόντια ταχύτητα υx και επιδρά επάνω του μόνο το βάρος του w.

ΟΡΙΖΟΝΤΙΑ ΒΟΛΗ ΣΚΙΕΡ

Για να μελετήσουμε την κίνηση του σκιέρ , επειδή είναι σύνθετη, πρέπει να εξετάσουμε το είδος της κίνησης στους άξονες xx’ και yy’ ξεχωριστά, σύμφωνα με την αρχή της ανεξαρτησίας των κινήσεων.

  Κάντε κλικ στο διάγραμμα

  Κάντε κλικ στο κουμπί

Ας δούμε αναλυτικά τι ισχύει σε κάθε άξονα στον xx' και στον yy'

  Κάντε κλικ στο διάγραμμα

  Κάντε κλικ στο διάγραμμα

Με βάση τα παραπάνω ,μπορούμε να υπολογίσουμε κάποια μεγέθη που αναλύουν περισσότερο την οριζόντια βολή.
 ΕΞΙΣΩΣΗ ΤΡΟΧΙΑΣ
Ψάχνουμε να βρούμε μια σχέση μεταξύ του x και του y. Aπό (2) είναι t=x/υ0 και αν κάνουμε αντικατάσταση στην (4) έχουμε

Alternative text for the image not set
είναι της μορφής y=αx2 δηλαδή μια παραβολή

  Κάντε κλικ στο διάγραμμα

ΧΡΟΝΟΣ ΠΤΩΣΗΣ (tπτώσης)  

Είναι ο χρόνος που χρειάζεται το σώμα για να φτάσει στο έδαφος.
Από τον τύπο (4) για y=H έχουμε


Alternative text for the image not set
ΒΕΛΗΝΕΚΕΣ (R)
Είναι η μέγιστη οριζόντια απόσταση που φτάνει το σώμα , έτσι από (2) για t=tπτώσης

Alternative text for the image not set
ΤΑΧΥΤΗΤΑ
Η ταχύτητα που έχει κάθε χρονική στιγμή το σώμα ,μπορεί να βρεθεί απο το διανυσματικό άθροισμα των ταχυτήτων στον xx' και yy' δηλαδή 
Alternative text for the image not set
Επειδή η ταχύτητα είναι διανυσματικό μέγεθος ,για να καθορίσουμε τη διεύθυνση της, πρέπει να βρούμε και τη εφαπτόμενη της γωνίας που σχηματίζει η ταχύτητα με τον ορίζοντα (όπως φαίνεται στο παρακάτω σχήμα)
Alternative text for the image not set

  Κάντε κλικ στην εικόνα

ΕΝΕΡΓΕΙΑΚΗ ΠΡΟΣΕΓΓΙΣΗ
 Η ταχύτητα μπορεί να υπολογιστεί επίσης εφαρμόζοντας την Αρχή Διατήρησης της Μηχανικής Ενέργειας .Έστω ένα μπαλάκι μάζας m ,εκτοξεύεται οριζόντια από ύψος Η με οριζόντια ταχύτητα υ x=υο όπως στο παρακάτω σχήμα .Αν θέλουμε να υπολογίσουμε την ταχύτητα με την οποία το μπαλάκι φτάνει στο έδαφος μπορούμε να θεωρήσουμε επίπεδο μηδενικής δυναμικής ενέργειας το έδαφος και να εφαρμόσουμε Α.Δ.Μ.Ε. από τη θέση Α στην θέση Γ. 
ΑΔΜΕ απο Α σε Γ 
ΕΜΗΧ(Α) =ΕΜΗΧ(Γ)=>ΚΑ+UB(A)=KΓ+UB(Γ) =>

½ mυο2+ mgH=½mυΓ2+0=>
υΓ=υεδάφους=√(υo2+2gH)

και για την διεύθυνση βρίσκουμε το συνθ=υΧ/υΓ.


  Κάντε κλικ στο διάγραμμα

  Κάντε κλικ στο διάγραμμα

ΕΦΑΡΜΟΓΗ

Στο διπλανό video ,έστω ότι το μπαλάκι εκτοξεύεται οριζόντια από την αθλήτρια Maria Sharapova με ταχύτητα 20m/s, από ύψος 80cm.
Υπολογίστε i) σε πόσο χρόνο θα φτάσει στο έδαφος και με πόση ταχύτητα ii) το βεληνεκές της βολής iii) την εξίσωση της τροχιάς της μπάλας iv) την μεταβολή της ορμής από την στιγμή που εκτοξεύτηκε μέχρι να φτάσει στο έδαφος (g=10m/s2)

Alternative text for the image not set
Alternative text for the image not set

  Κάντε κλικ στο διάγραμμα

ΣΥΓΚΡΙΣΗ ΧΡΟΝΟΥ ΠΤΩΣΗΣ ΣΕ ΟΡΙΖΟΝΤΙΑ ΒΟΛΗ ΚΑΙ ΕΛΕΥΘΕΡΗ ΠΤΩΣΗ
Δυο σώματα εκκινούν ταυτόχρονα απο το ίδιο ύψος ,το ένα εκτελεί ελεύθερη πτώση ,και το αλλό οριζόντια βολή ,ποιό θα φτάσει πρώτο στο έδαφος;
Δείτε το παρακάτω video απο 

Harvard Natural Sciences Lecture Demonstrations

https://www.youtube.com/watch?v=zMF4CD7i3hg&feature=youtu.be

ΠΟΛΛΑΠΛΗΣ ΕΠΙΛΟΓΗΣ

 Κάντε κλικ στη σωστή επιλογή

1. Οι κινήσεις που συνθέτουν την οριζόντια βολή είναι

Alternative text for the image not set

 Κάντε κλικ στη σωστή επιλογή

2. Στην οριζόντια βολή ,η αρχική ταχύτητα εκτόξευσης υx

Alternative text for the image not set

 Κάντε κλικ στη σωστή επιλογή

3. Όταν ένα σώμα εκτελεί οριζόντια βολή, τότε η κατακόρυφη του ταχύτητα υy

Alternative text for the image not set

 Κάντε κλικ στη σωστή επιλογή

4. H τροχιά που διαγράφει μια οβίδα που εκτοξεύεται από κανόνι με οριζόντια κάνη είναι

Alternative text for the image not set

 Κάντε κλικ στη σωστή επιλογή

5. Για τα μεγέθη επιτάχυνση και ταχύτητα μιας πέτρας που κάνει οριζόντια βολή ισχύει οτι

Alternative text for the image not set

 Κάντε κλικ στη σωστή επιλογή

6. Στην οριζόντια βολή η διεύθυνση της ταχύτητας είναι κάθε χρονική στιγμή

Alternative text for the image not set

 Κάντε κλικ στη σωστή επιλογή

7. Σε μια οριζόντια βολή ισχύει η αρχή διατήρησης της

Alternative text for the image not set

 Κάντε κλικ στη σωστή επιλογή

8. Ένα σώμα βάλλεται οριζόντια από ύψος Η=180m .Θα φτάσει στο έδαφος σε χρόνο.

Alternative text for the image not set

 Κάντε κλικ στη σωστή επιλογή

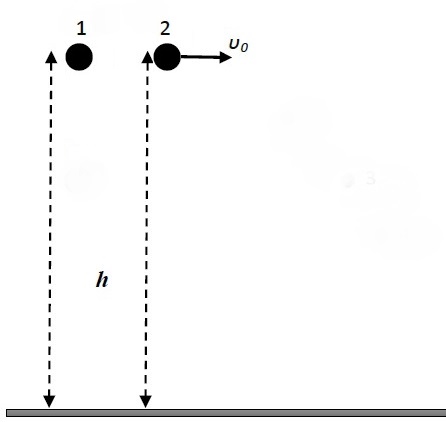
9. Σφαίρα (1) αφήνεται να πέσει από μικρό ύψος Η, εκτελώντας ελεύθερη πτώση. Μια ίδια σφαίρα (2) βάλλεται από το ίδιο ύψος με οριζόντια ταχύτητα μέτρου υo. Εάν υ1 και υ2 είναι τα μέτρα των ταχυτήτων των δύο σφαιρών τη χρονική στιγμή που φτάνουν στο έδαφος, τότε ισχύει:

Alternative text for the image not set

 Κάντε κλικ στη σωστή επιλογή

10. Με βάση τα δεδομένα της ερώτησης 9. Έστω t1 και t2 οι χρόνοι που κάνουν η πρώτη και η δεύτερη σφαίρα αντίστοιχα να φτάσουν στο έδαφος. Τότε ισχύει:

Alternative text for the image not set

 Κάντε κλικ στη σωστή επιλογή

11. Από πολεμικό αεροπλάνο που πετάει με σταθερή ταχύτητα υ, σε ύψος Η, αφήνεται να πέσει μια βόμβα . Αν δεν υπάρχουν τριβές τότε ο πιλότος του αεροπλάνου βλέπει ότι η τροχιά της βόμβας είναι:

Alternative text for the image not set

 Κάντε κλικ στη σωστή επιλογή

12. Δύο σφαίρες Σ1 και Σ2 εκτοξεύονται οριζόντια με την ίδια ταχύτητα από σημεία Α και Β αντίστοιχα που βρίσκονται στην ίδια κατακόρυφο και σε ύψη από το έδαφος Η και h αντίστοιχα για τα οποία ισχύει Η=16h Αν τα βεληνεκή , είναι R1 και R2 αντίστοιχα τότε ισχύει:

Alternative text for the image not set

 Κάντε κλικ στη σωστή επιλογή

13. Από σημείο Α. που βρίσκεται σε ύψος h πάνω από το έδαφος, βάλλεται οριζόντια μικρή πέτρα με αρχική ταχύτητα μέτρου υο=12m/s . Αν τη στιγμή της εκτόξευσης η βαρυτική δυναμική της ενέργεια είναι τριπλάσια της κινητικής της ενέργειας ,τότε το μέτρο της ταχύτητας της όταν φτάνει στο έδαφος είναι

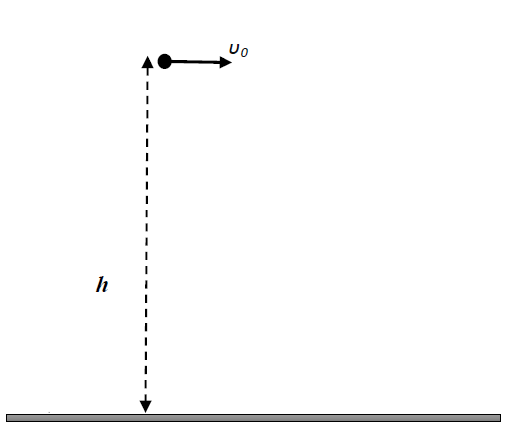
Alternative text for the image not set

 Κάντε κλικ στη σωστή επιλογή

14. Για τα δεδομένα της ερώτησης 13 το βεληνεκές της πέτρας ισούται με

Alternative text for the image not set

 Κάντε κλικ στη σωστή επιλογή

15. Από σημείο Α που βρίσκεται σε ύψος Η πάνω από το έδαφος βάλλεται οριζόντια ένα σώμα με αρχική ταχύτητα μέτρου υo.Τη στιγμή που το μέτρο της ταχύτητας υx είναι ίσο με το μέτρο της υy o λόγος των συντεταγμένων του, y/x του είναι

Alternative text for the image not set

 Κάντε κλικ στη σωστή επιλογή

16. Από σημείο A που βρίσκεται σε ύψος Η πάνω από την επιφάνεια λίμνης, βάλλεται οριζόντια ένα λεμόνι μάζας m με αρχική ταχύτητα μέτρου υο, έχοντας κινητική ενέργεια Κο. Τη στιγμή που η κινητική ενέργεια του λεμονιού έχει διπλασιαστεί, ο λόγος των μέτρων των ταχυτήτων υx/υy είναι ίσος με:

Alternative text for the image not set

 Κάντε κλικ στη σωστή επιλογή

17. Στο παρακάτω σχήμα ,αφήνεται σώμα μάζας m να κινηθεί χωρίς τριβές από ανώτερο σημείο τεταρτοκύκλιου ακτίνας r .Το βεληνεκές της οριζόντιας βολής που θα εκτελέσει είναι

Alternative text for the image not set

ΣΥΜΠΛΗΡΩΣΗΣ ΚΕΝΟΥ

  Απαντήστε σε κάθε ερώτηση

1. Ένα σώμα m=0,1kg εκτελεί οριζόντια βολή με αρχική οριζόντια ταχύτητα υο, και όταν φτάνει στο έδαφος είναι x=600m και y=500m .Το βεληνεκές του είναι R=____ m
2. Η αρχική ταχύτητα του είναι υο=____ m/s (ερώτηση 1)
3. Ο συνολικός χρόνος κίνησης ισούται με t=____ s (ερώτηση 1)
4 .Το μέτρο της ταχύτητας του ,τη στιγμή t=1s είναι υ1=____ m/s (ερώτηση 1)
5 .Το έργο του βάρους του ,κατά την πτώση είναι Ww= ____ J (ερώτηση 1)
6. Ο ρυθμός μεταβολής της κινητικής του ενέργειας ,τη στιγμή που φτάνει στο έδαφος είναι dK/dt = ____ J/s (ερώτηση 1)
7. Μία μπάλα εκτοξεύεται οριζόντια από ύψος 20 m. Η αντίσταση του αέρα είναι αμελητέα. Αν το βεληνεκές της βολής είναι 80 m, η αρχική ταχύτητα της μπάλας είναι ____ m/s
8. Δύο μικρές σφαίρες (1) και (2) εκτοξεύονται ταυτόχρονα τη χρονική στιγμή t = 0s οριζόντια από ύψη H(1), H(2) αντίστοιχα, που βρίσκονται στην ίδια κατακόρυφο. Οι αρχικές οριζόντιες ταχύτητες των δύο σφαιρών συνδέονται με τη σχέση: υ(1) = 3υ(2) . Αν τα σώματα έχουν το ίδιο βεληνεκές , τότε τα ύψη H(1), H(2) συνδέονται με τη σχέση:H(2)/H(1)= ____
9 . Από ύψος h εκτοξεύεται οριζόντια ένα σώμα με ταχύτητα 20 m/s. Το σώμα συναντά το έδαφος σε χρόνο 2 s. Η γωνία που σχηματίζει το διάνυσμα της ταχύτητας με το διάνυσμα της κατακόρυφης συνιστώσας της ταχύτητας είναι θ= ____ rad
10. Δύο σώματα Α και Β μικρά σε διαστάσεις, έχουν μάζες mΑ και mΒ = mΑ/4, αντίστοιχα. Τα Α και Β εκτοξεύονται ταυτόχρονα οριζόντια με ταχύτητες υ0(Α) και υ0(Β) = 2υ0(Α), από ύψη hΑ και hΒ = 4.hΑ, αντίστοιχα. Η αντίσταση του αέρα είναι αμελητέα. Ο λόγος των κινητικών ενεργειών ΚΑ / ΚΒ με τις οποίες φτάνουν στο έδαφος είναι ίσος με ____

ΣΩΣΤΟ-ΛΑΘΟΣ

ΕΡΩΤΗΣΗ Α
Σφαίρα (1) αφήνεται να πέσει από ύψος Η εκτελώντας ελεύθερη πτώση και ταυτόχρονα μια όμοια σφαίρα (2) βάλλεται από το ίδιο ύψος με οριζόντια ταχύτητα μέτρου uo, Ποιες από τις παρακάτω προτάσεις είναι σωστές και ποιες λάθος;
Alternative text for the image not set

  Ταξινόμηση ως αληθής ή ψευδής

  • 1. Κάθε χρονική στιγμή οι σφαίρες έχουν ίδια ταχύτητα

  • 2. Οι σφαίρες θα φτάσουν ταυτόχρονα στο έδαφος

  • 3. Οι σφαίρες έχουν κάθε χρονική στιγμή ίδια ορμή

  • 4. Οι σφαίρες έχουν κάθε στιγμή την ίδια δυναμική βαρυτική ενέργεια

  • 5. Οι σφαίρες κάθε στιγμή έχουν ίδια επιτάχυνση.

ΕΡΩΤΗΣΗ Β
Για ένα σώμα που εκτελεί οριζόντια βολή από ύψος Η με οριζόντια ταχύτητα υο ,ποιες από τις παρακάτω προτάσεις είναι σωστές και ποιες λάθος;

  Ταξινόμηση ως αληθής ή ψευδής

  • 1. Η οριζόντια ταχύτητα παραμένει σταθερή

  • 2. Η ταχύτητα έχει ίδια κατεύθυνση με την επιτάχυνση

  • 3. Η κατακόρυφη συνιστώσα της ταχύτητας μειώνεται με το χρόνο

  • 4. Το διάνυσμα του ρυθμού μεταβολής της ορμής είναι κατακόρυφο

  • 5. Το μέτρο της μεταβολής της ορμής είναι ανάλογο του χρόνου πτώσης

  • 6. Αν διπλασιάσουμε την ταχύτητα εκτόξευσης θα διπλασιαστεί και το βεληνεκές

  • 7. Αν διπλασιάσουμε την ταχύτητα εκτόξευσης θα διπλασιαστεί και ο χρόνος πτώσης

  • 8. Αν τετραπλασιάσουμε την ταχύτητα εκτόξευσης θα διπλασιαστεί η κινητική ενέργεια με την οποία θα φτάσει στο έδαφος

  • 9. Ο ρυθμός μεταβολής της κινητικής ενέργειας του σώματος τη στιγμή της εκτόξευσης είναι μηδέν

VOLLEYBALL

Alternative text for the image not set