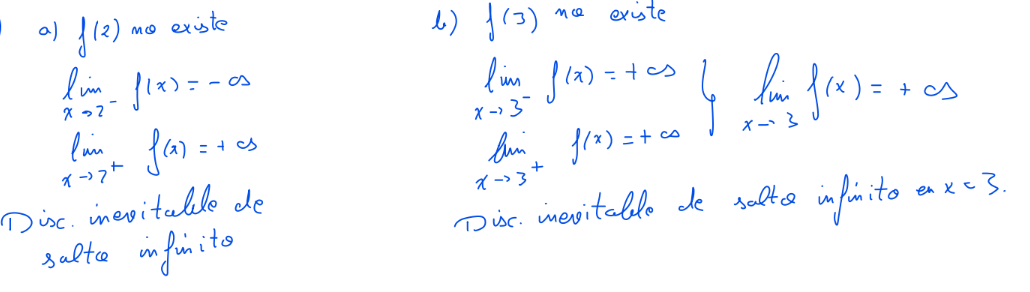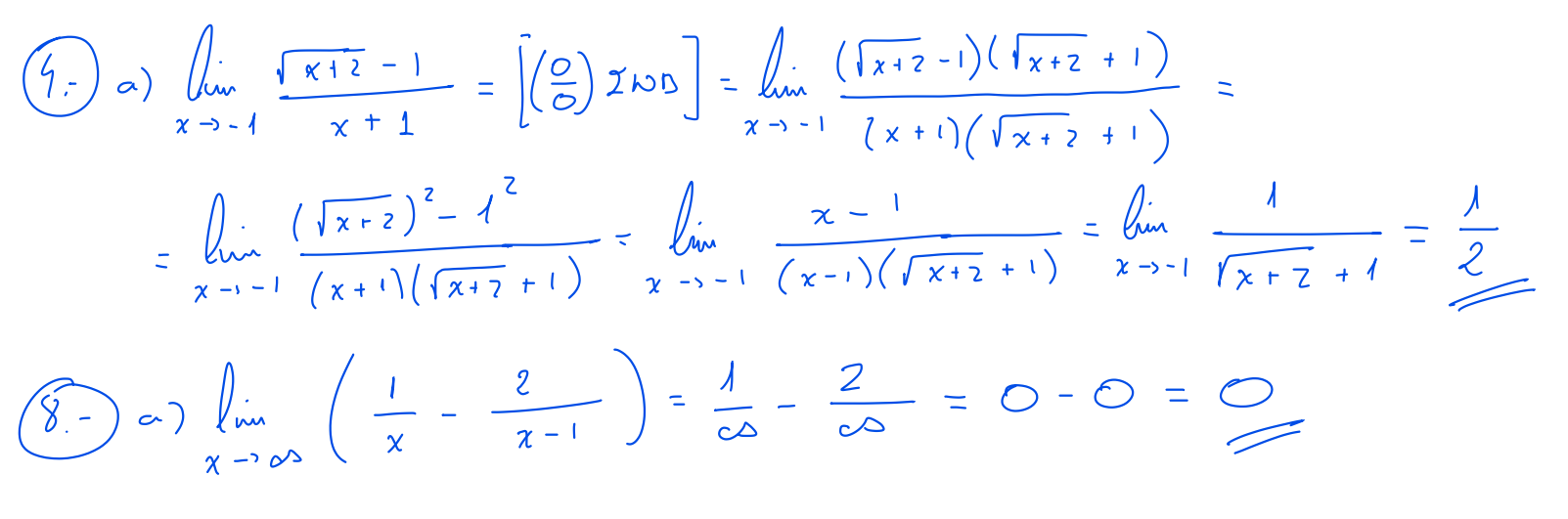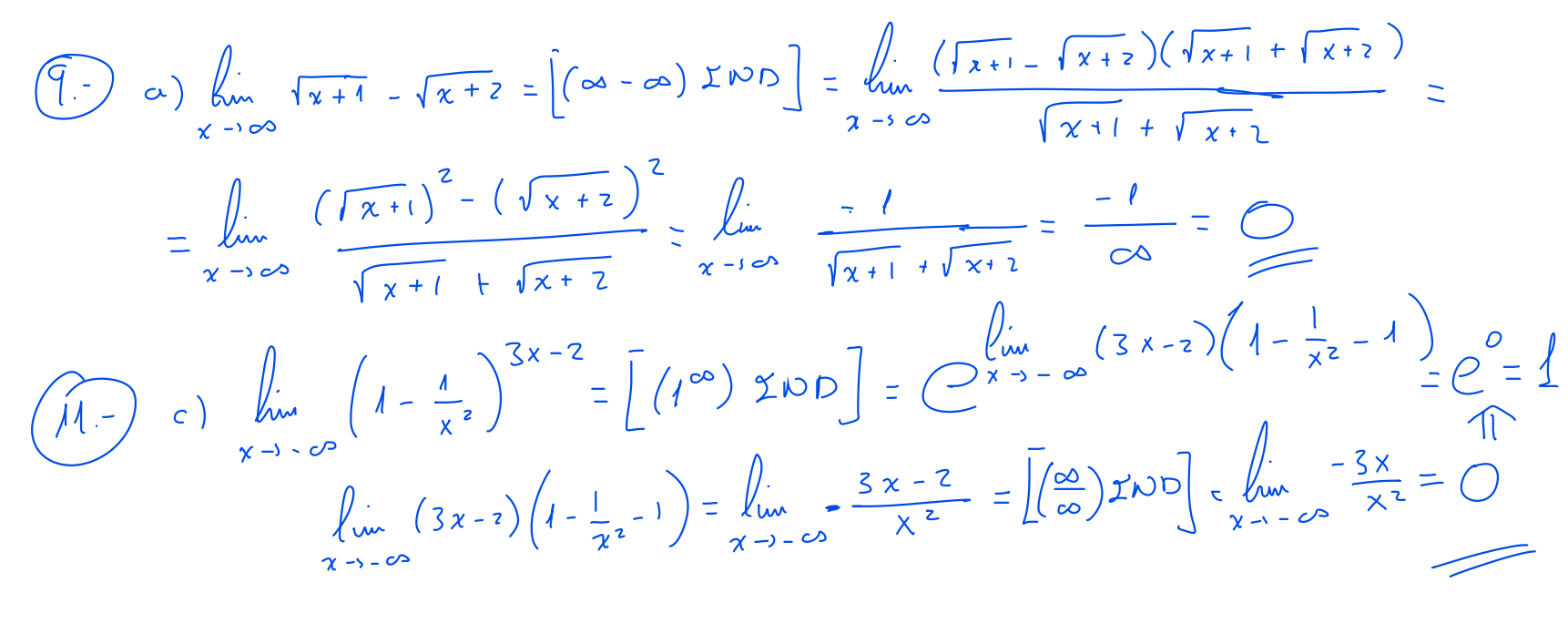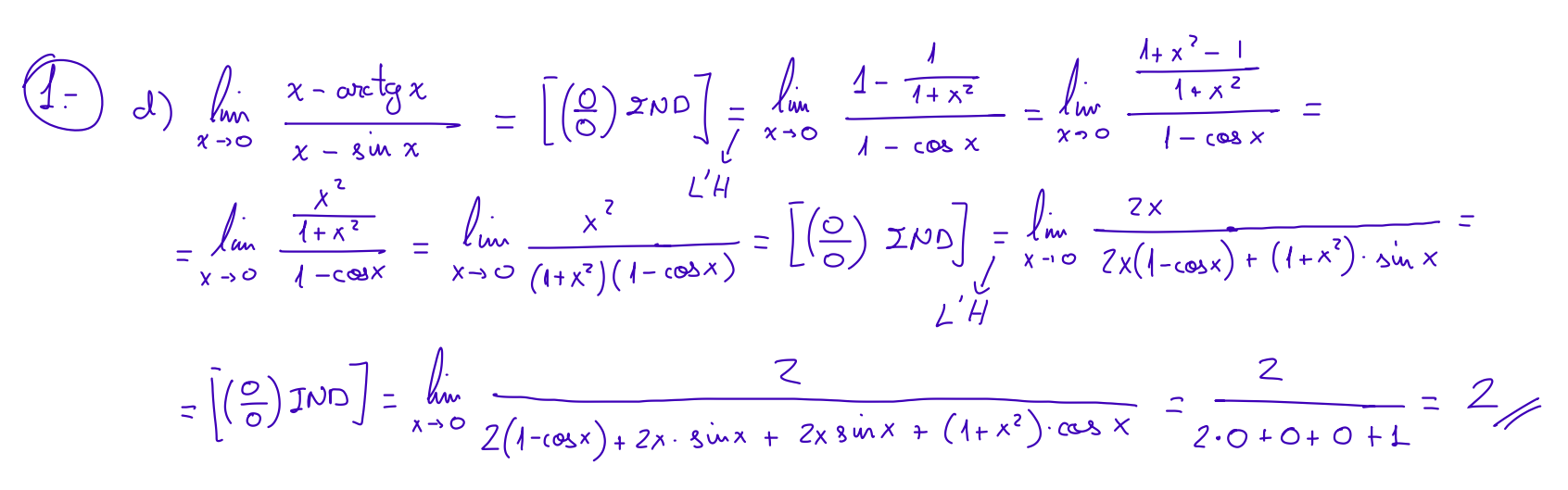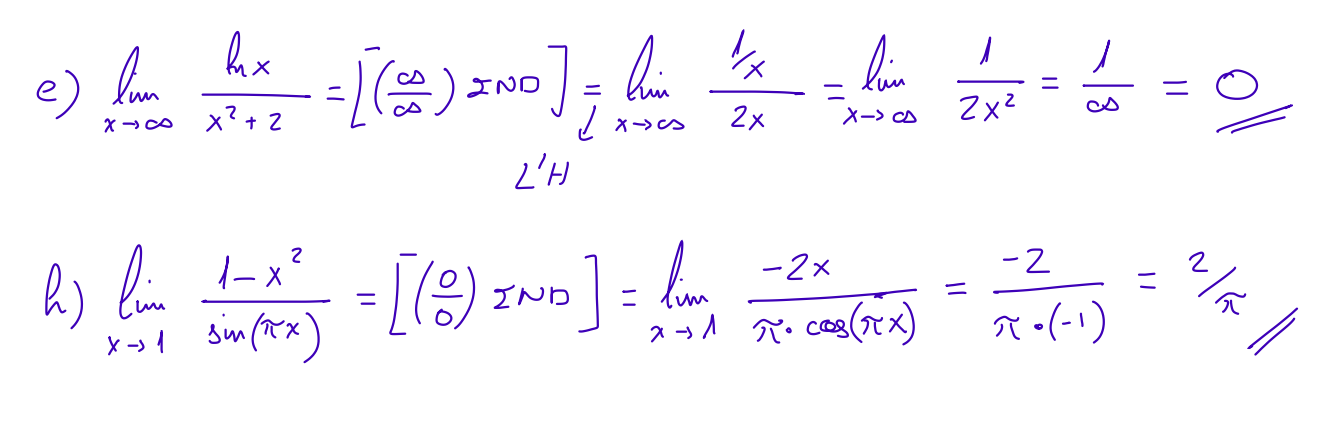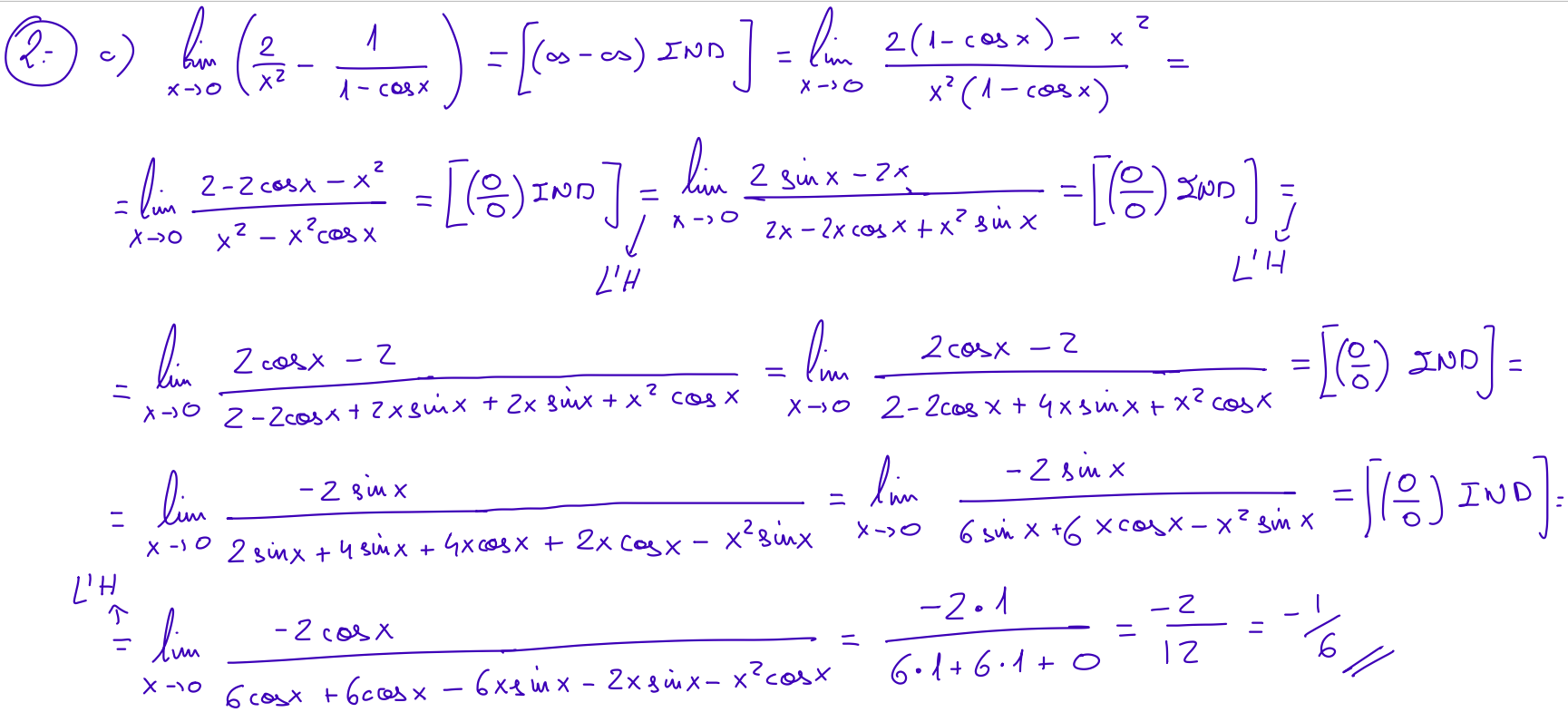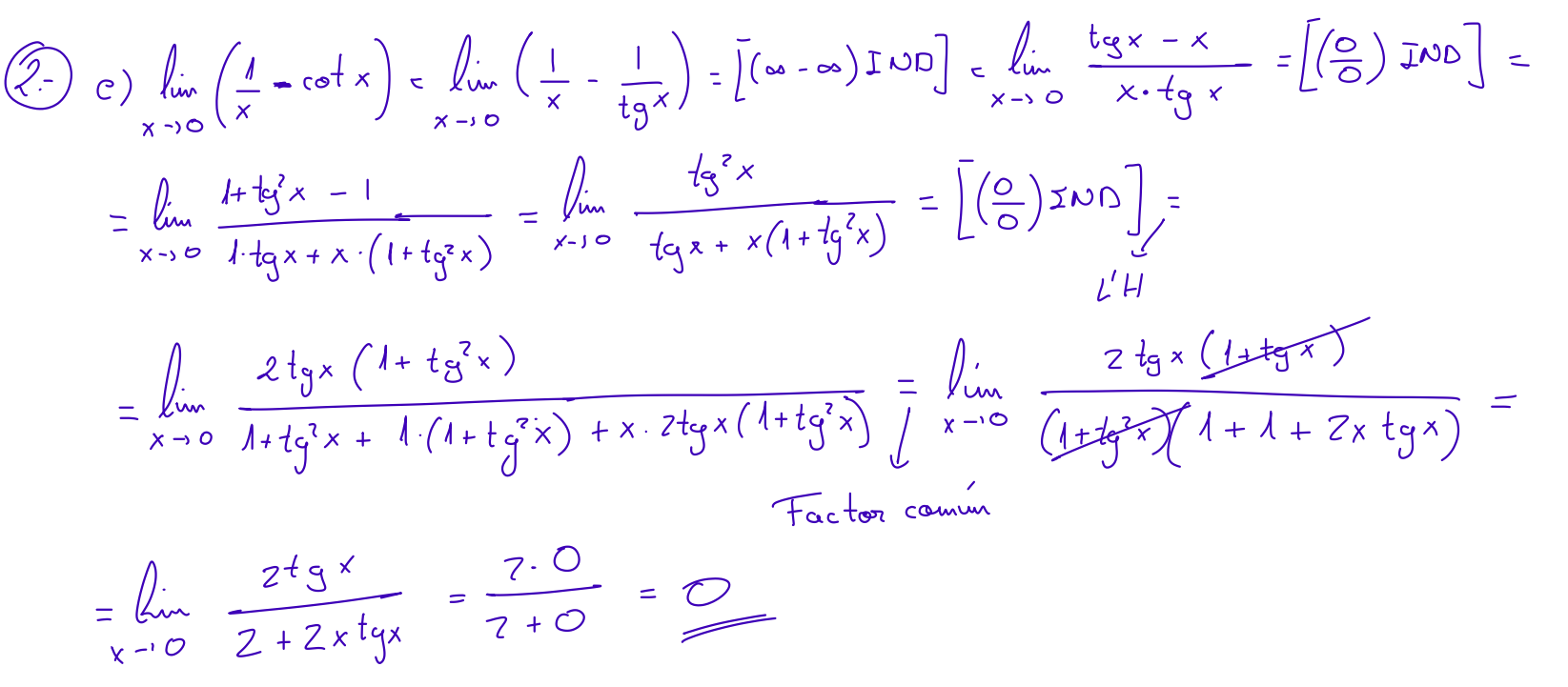MATEMÁTICAS II - Bloque 1: Funciones. Cálculo Diferencial

Funciones. Propiedades y características

Funciones y sus características

Una función real de variable real es una regla o correspondencia que asigna a cada número real \(x\) un único valor \(f(x)\) que también es un número real.

Normalmente, una función se representa mediante el siguiente esquema: $$\begin{array}{cccc} f:&\mathbb{R}&\longrightarrow&\mathbb{R}\\&x&\longmapsto&f(x)\end{array}$$

Las funciones tienen multitud de propiedades y características. Algunas de ellas, como la continuidad o derivabilidad son de gran complejidad. Por el momento, vamos a recordar las características más básicas de las funciones, base del resto del tema.

Texto alternativo de la imagen no establecido

  EJEMPLO DE FUNCIÓN:

Literal: consiste en definir la función mediante una expresión que emplee el lenguaje habitual. En este caso vamos a definir la función que calcula el cuadrado de un número real \(x\).

Algebraica: \( f(x) = x^2 \)

\(x\) representa la variable independiente, a la que se pueden dar los valores que se quiera. Si queremos calcular los valores de la función en los puntos \(x=1, x=2, x=-2 \dots\) se representa:

                                                               \(f(1) = 1, f(2) = 4, f(-2) = 4 \dots\)

Tabla de valores: 

\(x\) 0 1 2 3 ...
\(f(x)\) 0 1 4 9 ...
Si representamos los puntos \((x, f(x))\) en los ejes de coordenadas obtenemos la gráfica de la función.
Función cuadrática

  CARACTERÍSTICAS DE LAS FUNCIONES:

El dominio de una función real es el subconjunto de números reales para los que existe (se puede calcular) la función. Concretamente:

                                          \(Dom ~ f = \left\{x\in \mathbb{R}: \exists f(x) \right\}\)

Recuerda que a la hora de calcular el dominio hay ciertos tipos de funciones de especial interés: \(\dfrac{f(x)}{g(x)}, \ \sqrt[n]{f(x)}, \ \log_a f(x)\)...

Intuitivamente, podemos pensar en el dominio como aquellos puntos del eje X que quedan por encima o por debajo de la gráfica de la función.

Texto alternativo de la imagen no establecido

Es el conjunto de valores que toma \(f(x)\) para cada \(x\) de su dominio.

Intuitivamente, podemos pensar en la imagen como el conjunto de puntos del eje Y que quedan a la derecha o a la izquierda de la gráfica de la función.

Texto alternativo de la imagen no establecido

\(f(x)\) es simétrica par si: \(f(x) = f(-x)\)

Texto alternativo de la imagen no establecido

\(f(x)\) es simétrica impar si: \(f(-x) = -f(x)\)

Texto alternativo de la imagen no establecido

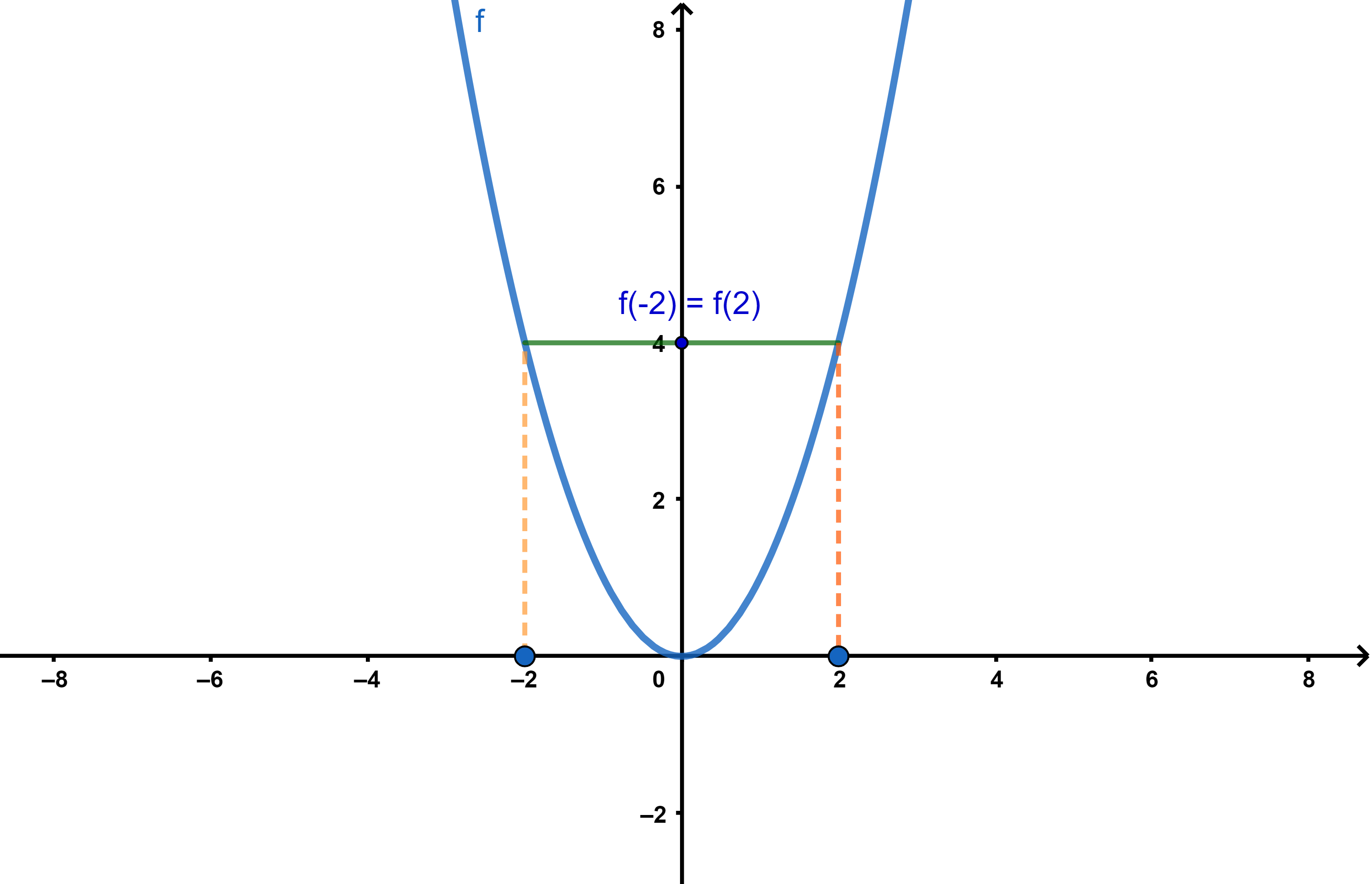
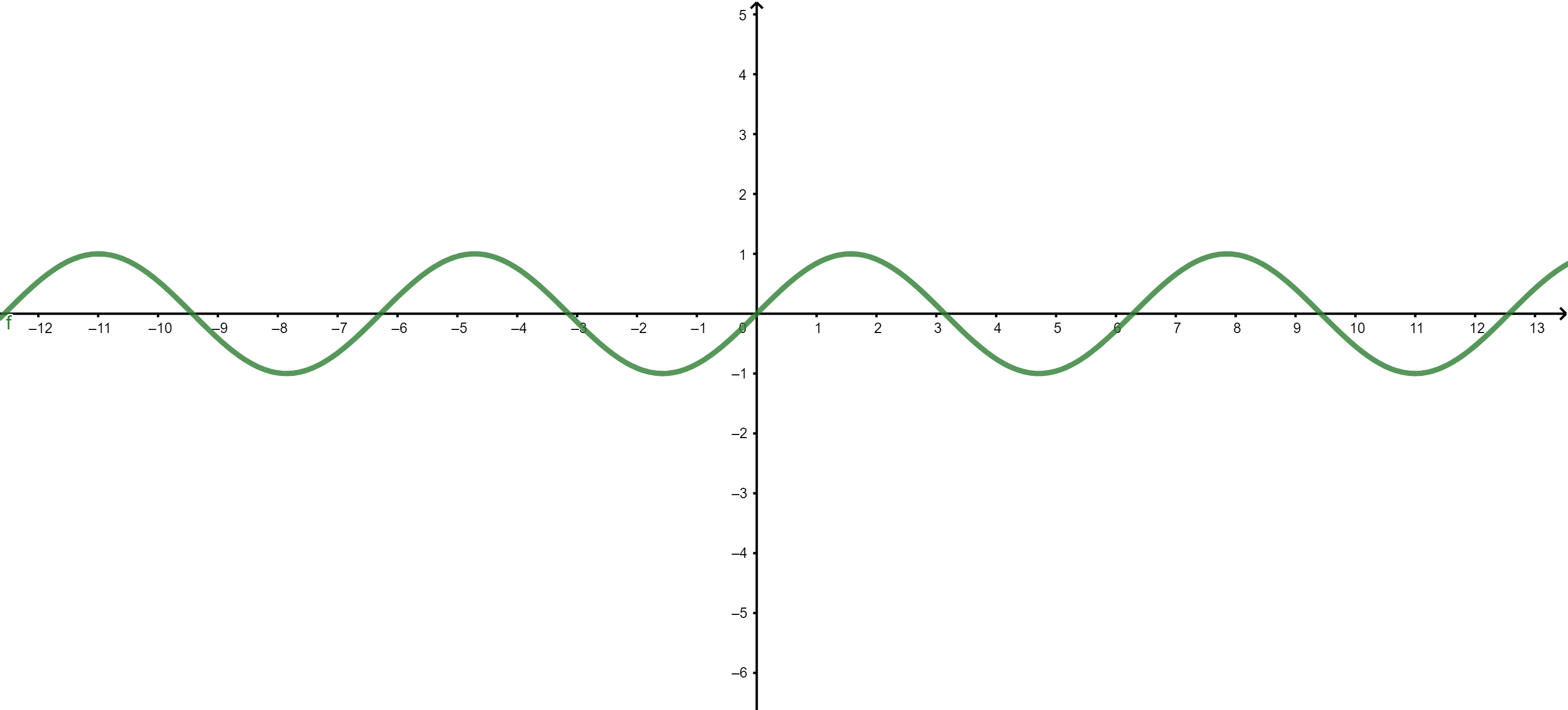
Una función se dice periódica si existe un cierto número \(T\), conocido como periodo, para el cual \(f(x+T) = f(x)\) para cada valor \(x\) que tome la función.

Los ejemplos más habituales de funciones periódicas los encontramos con las funciones trigonométricas (seno, coseno y tangente), aunque no son los únicos.

Texto alternativo de la imagen no establecido

EJE X (o abscisas): Son aquellos puntos de la gráfica en los que \(y=0\), por tanto tendrán la forma \((\underline{},0)\).

Para calcularlos hemos de resolver la ecuación \(f(x) = 0\).

EJE Y (u ordenadas): Es el único punto de la gráfica para el que \(x=0\), por tanto tendrán la forma \((0,\underline{})\).

Para obtenerlo hemos de calcular \(f(0)\) (en caso de que sea posible).

El crecimiento y decrecimiento se describirá con intervalos de valores en el eje de abscisas en los que, al movernos de izquierda a derecha, la gráfica de la función sube o baja (respectivamente).

Intuitivamente, diremos que una función es continua cuando podemos trazar su gráfica sin levantar el lápiz del papel. Cuando una función no es continua en un punto \(x=a\), decimos que es discontinua. Más adelante daremos una definición más precisa de función continua y estudiaremos los tipos de discontinuidad.

Una función tiene una tendencia horizontal en \(+\infty\) (o en \(-\infty\)) hacia \(y=b\) cuando a medida que el valor de \(x\) aumenta (o disminuye) indefinidamente, el valor de \(f(x)\) se aproxima infinitamente a \(b\). En cualquier caso, diremos que \(y=b\) es una asíntota horizontal.

Texto alternativo de la imagen no establecido

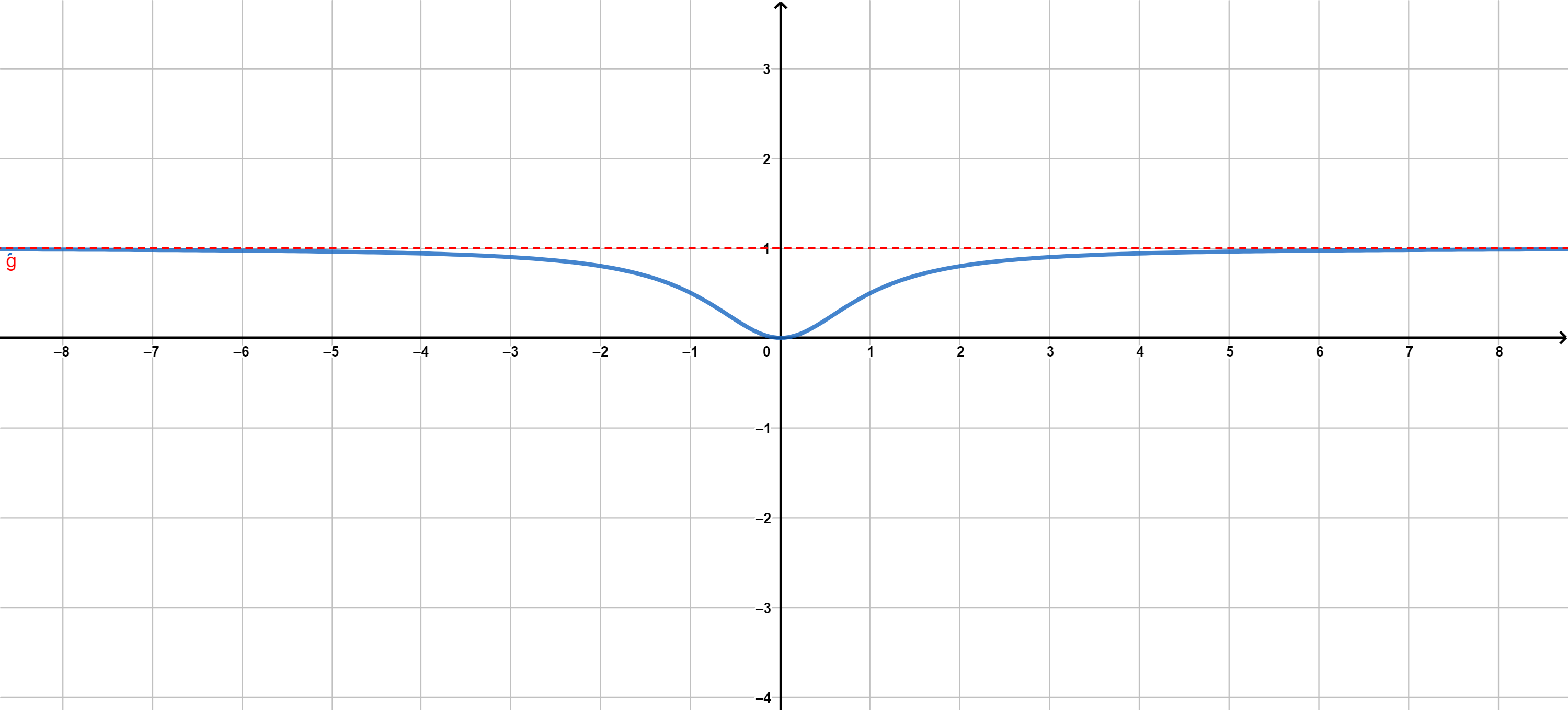
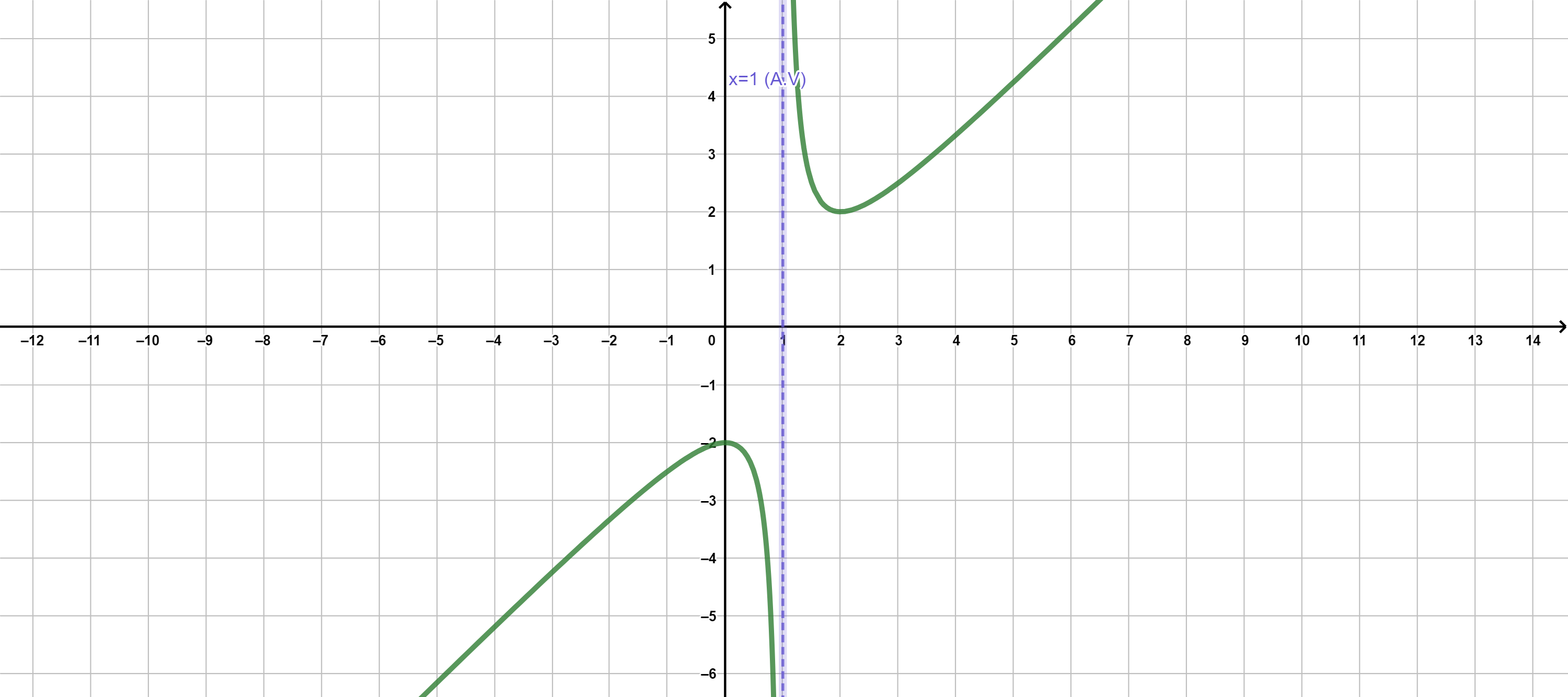
Una función tiene una tendencia vertical en \(x=a\) por la izquierda (o por la derecha) cuando a medida que el valor de \(x\) se aproxima a \(x=a\) por la izquierda (o por la derecha), el valor de \(f(x)\) crece o decrece indefinidamente. En cualquier caso, diremos que \(x=a\) es una asíntota vertical.

Texto alternativo de la imagen no establecido

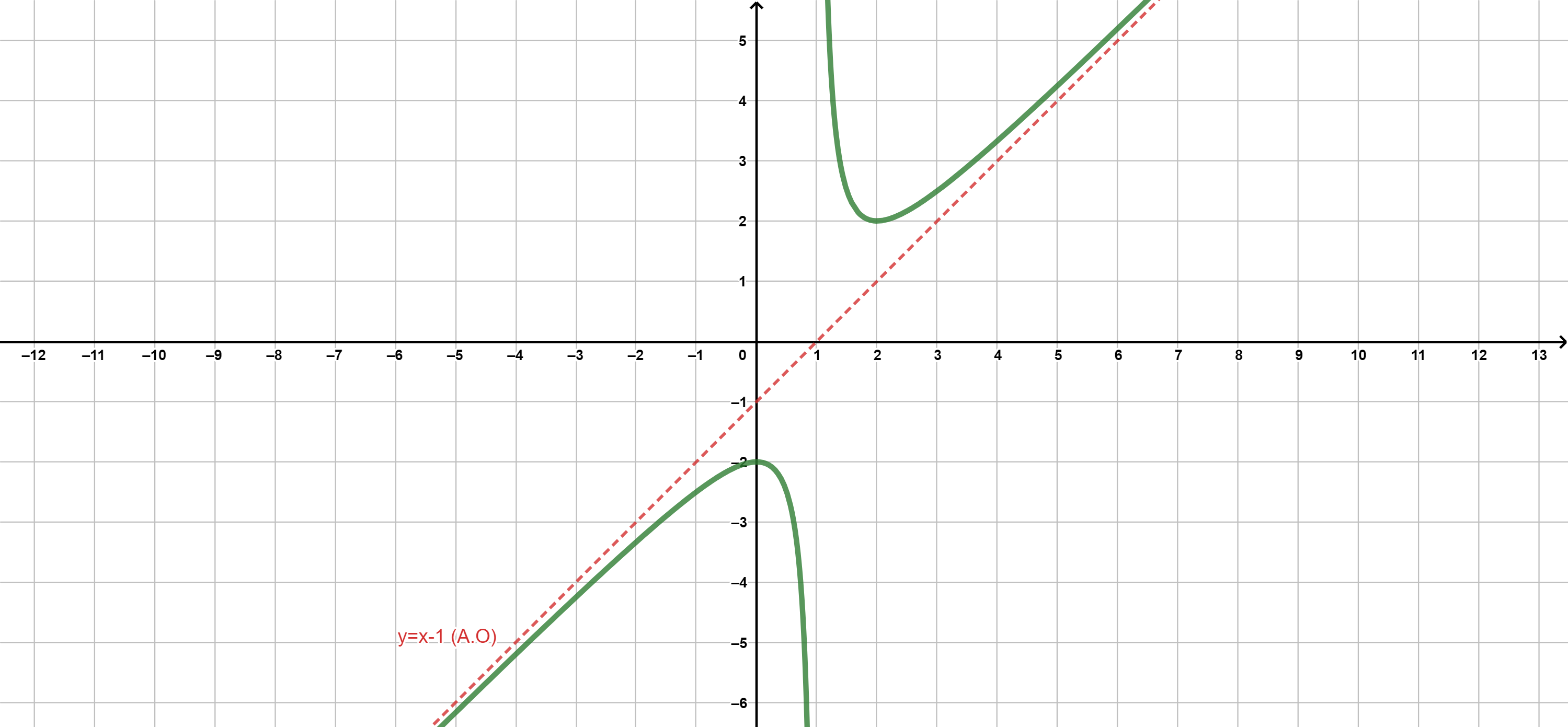
Una función tiene una asíntota oblicua de la forma \(y=mx+n\) en \(+\infty\) (o en \(-\infty\)) cuando a medida que el valor de \(x\) aumenta (o disminuye) \(f(x)\) se aproxima a la recta que define la asíntota.

Texto alternativo de la imagen no establecido
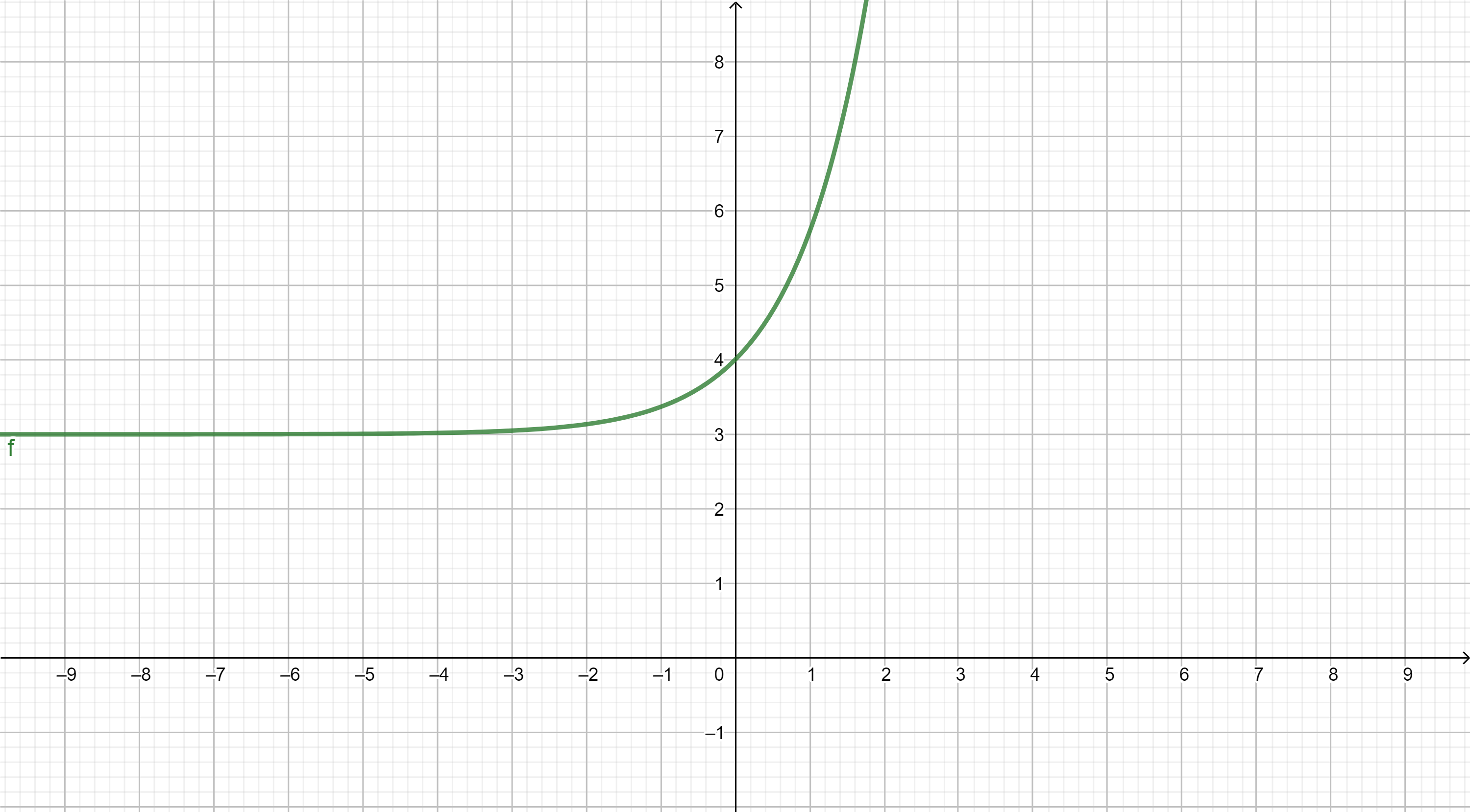
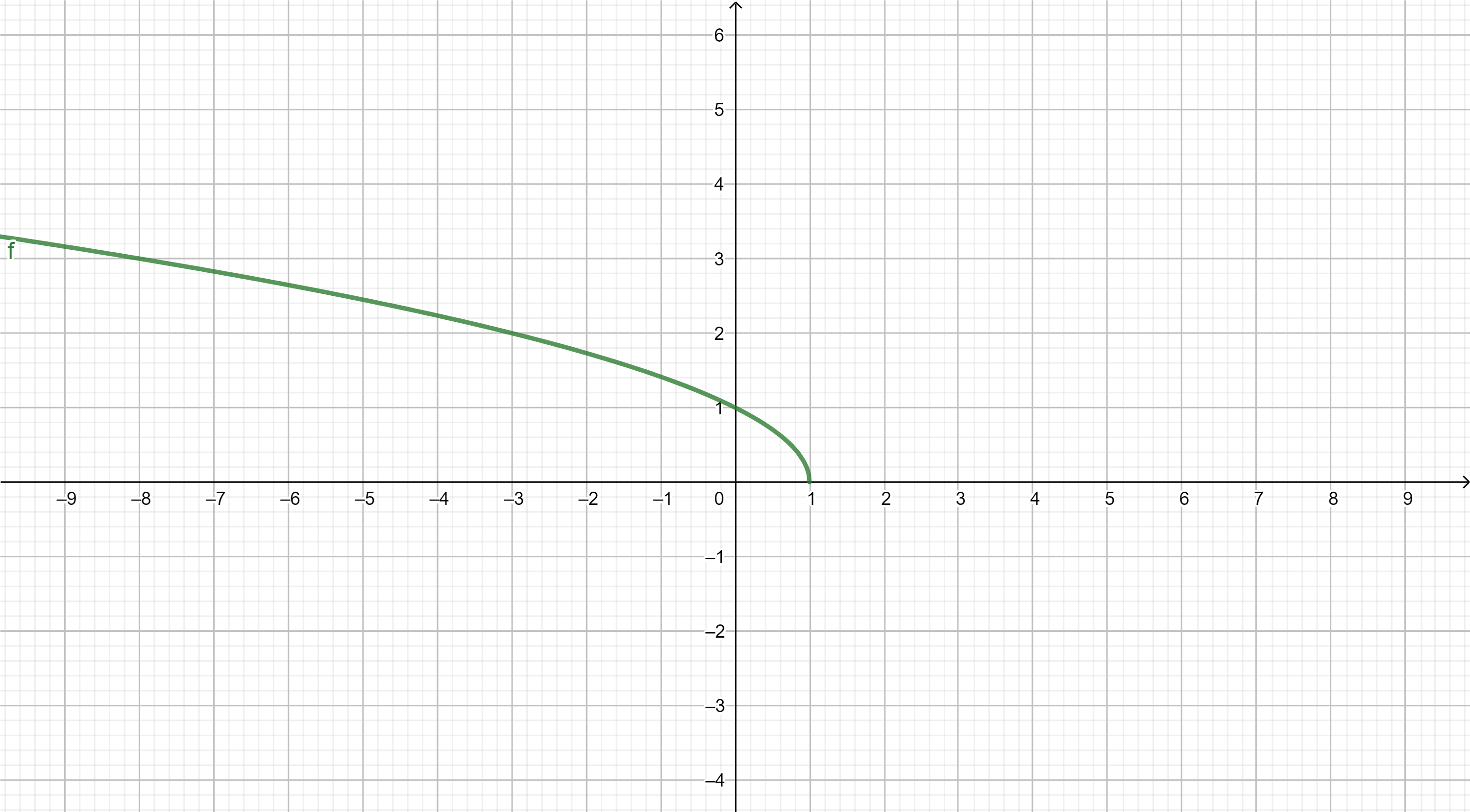
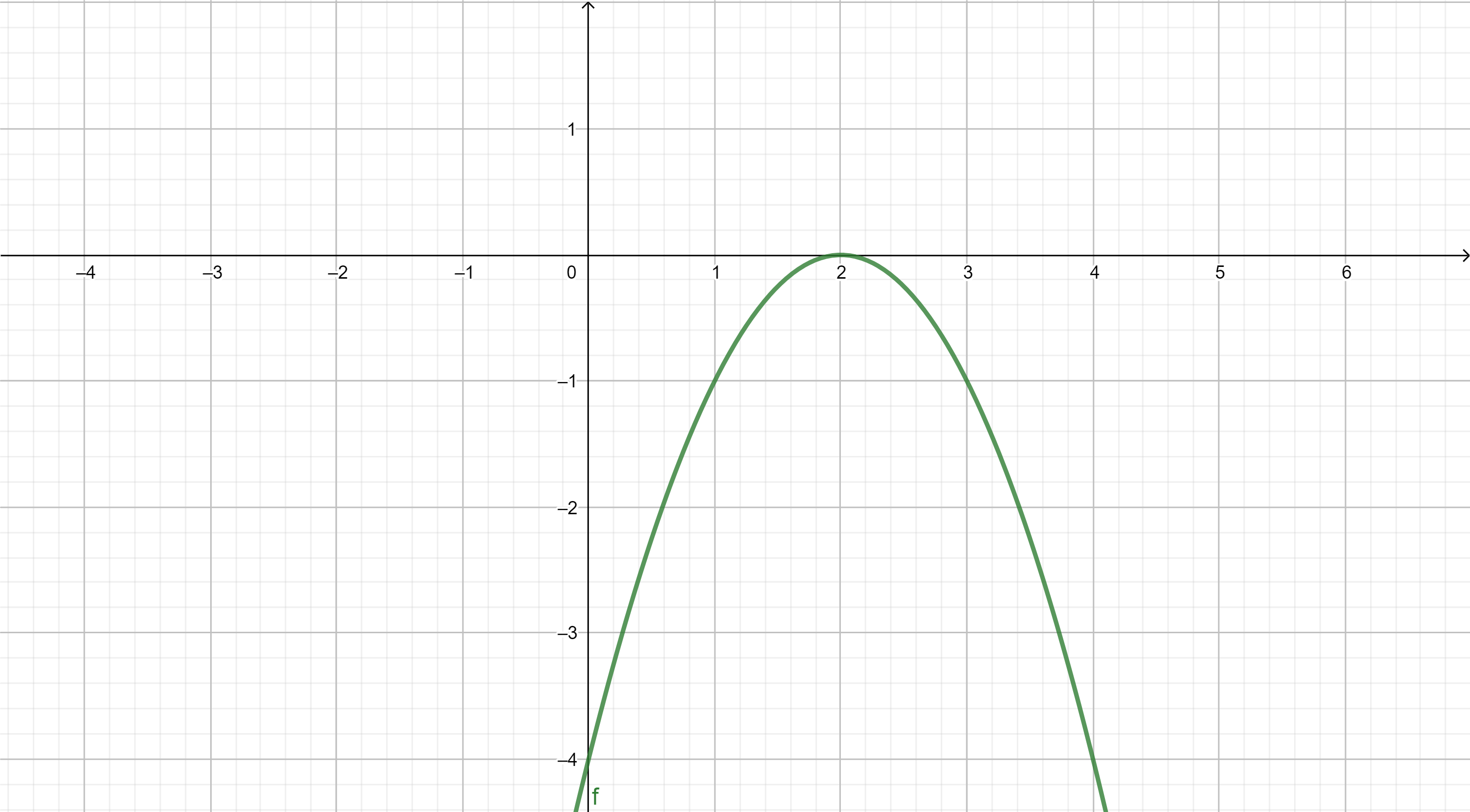
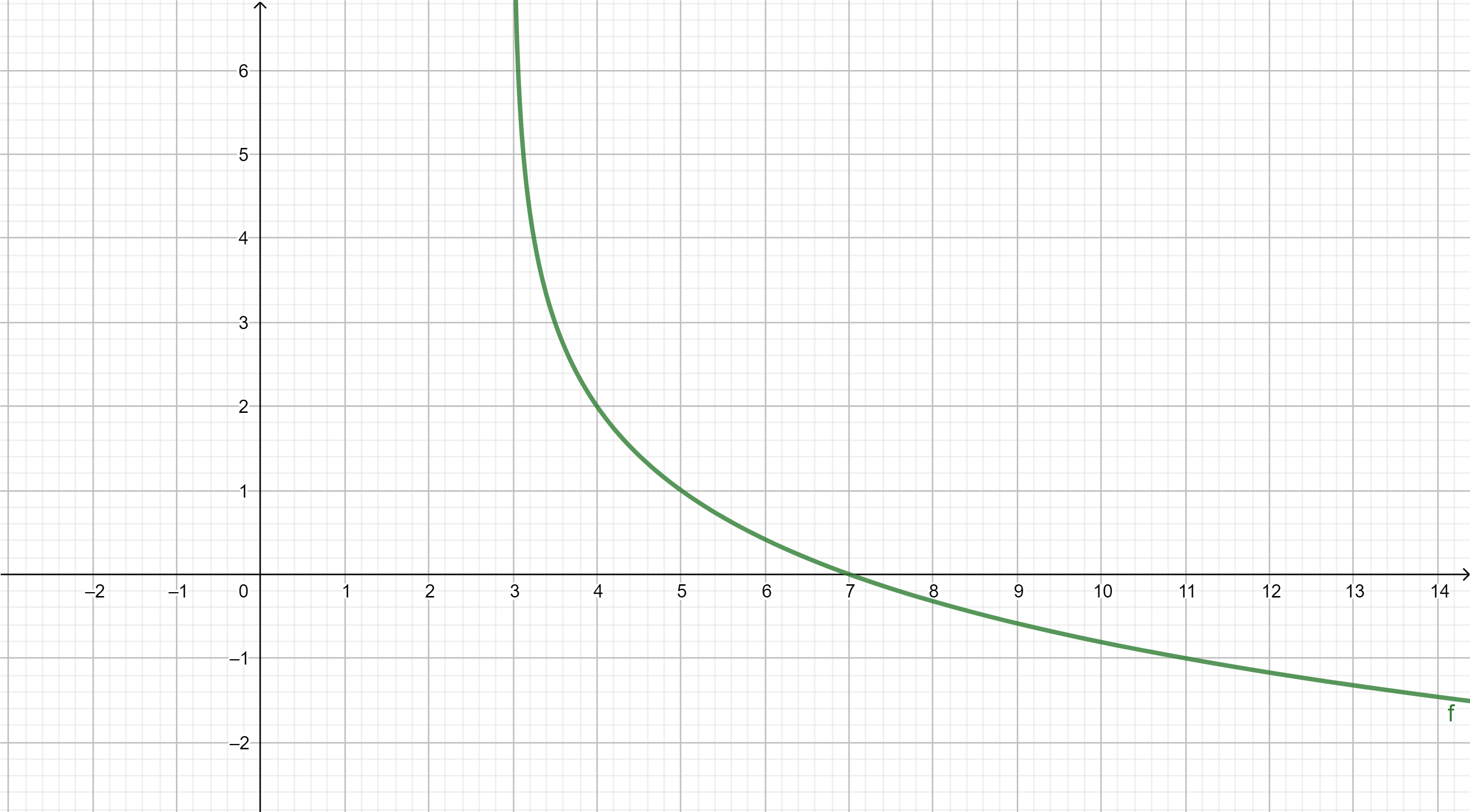
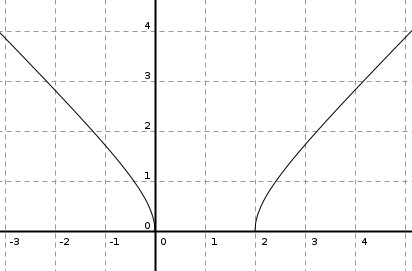
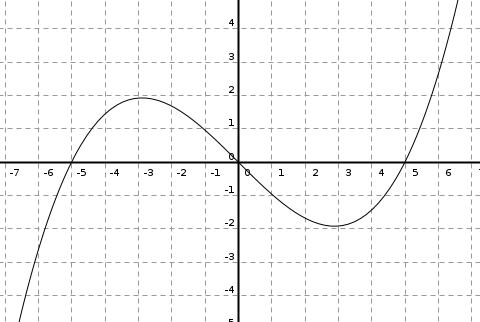
Funciones elementales

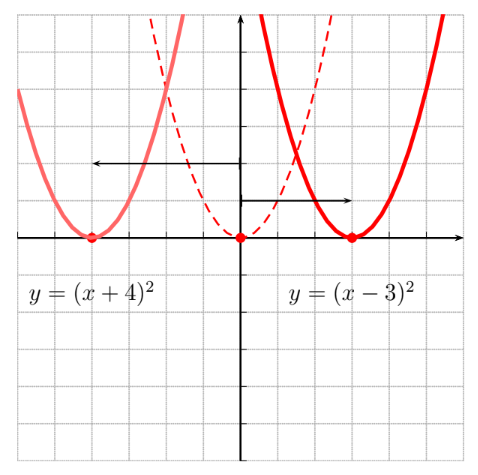
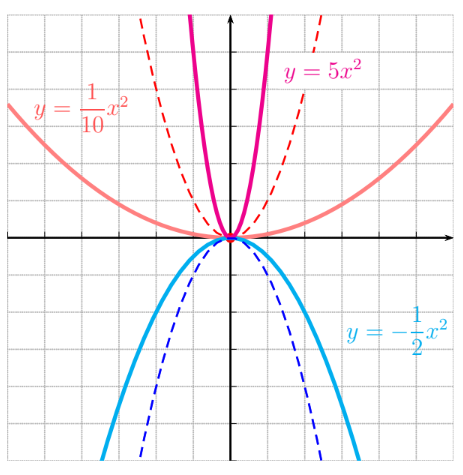
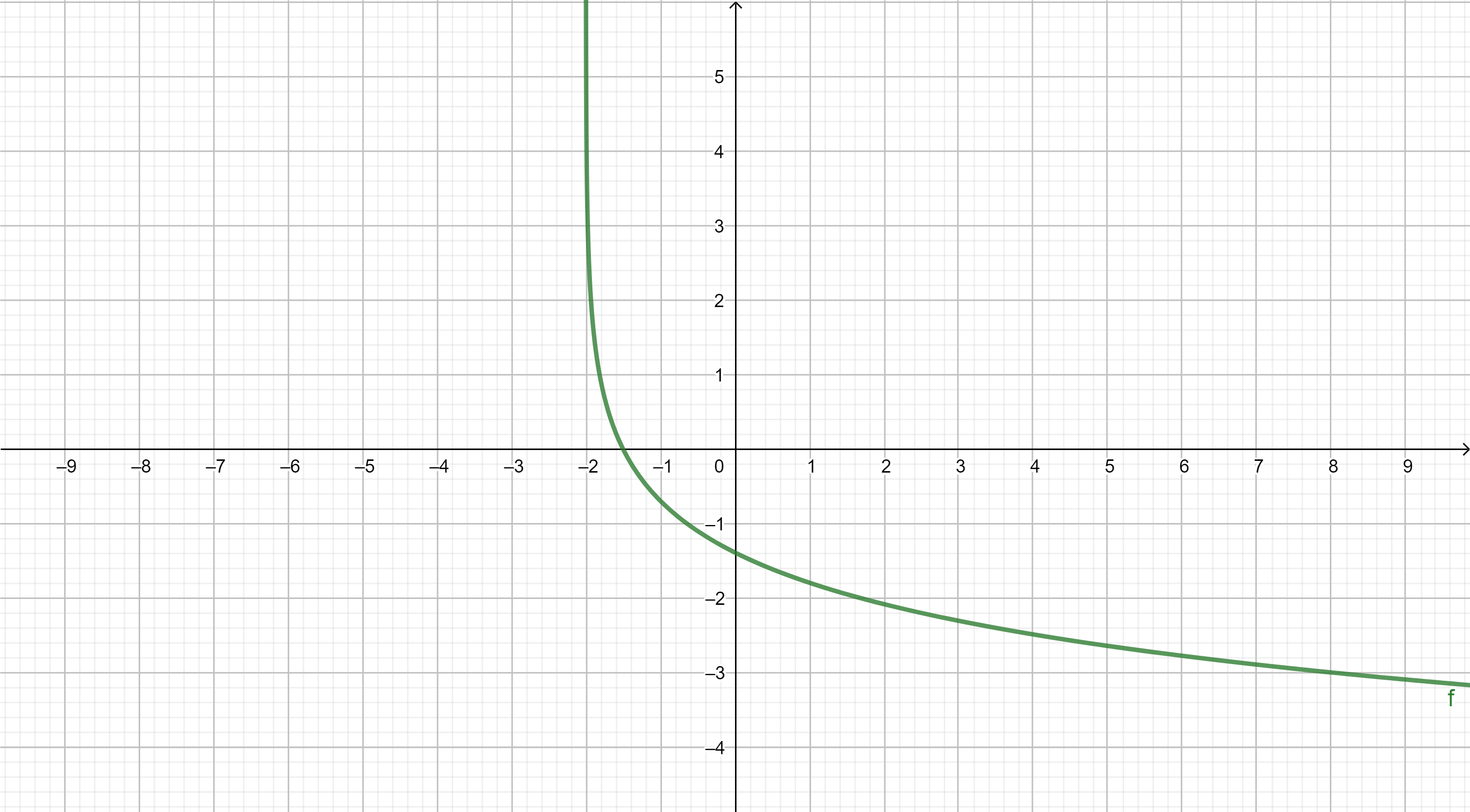
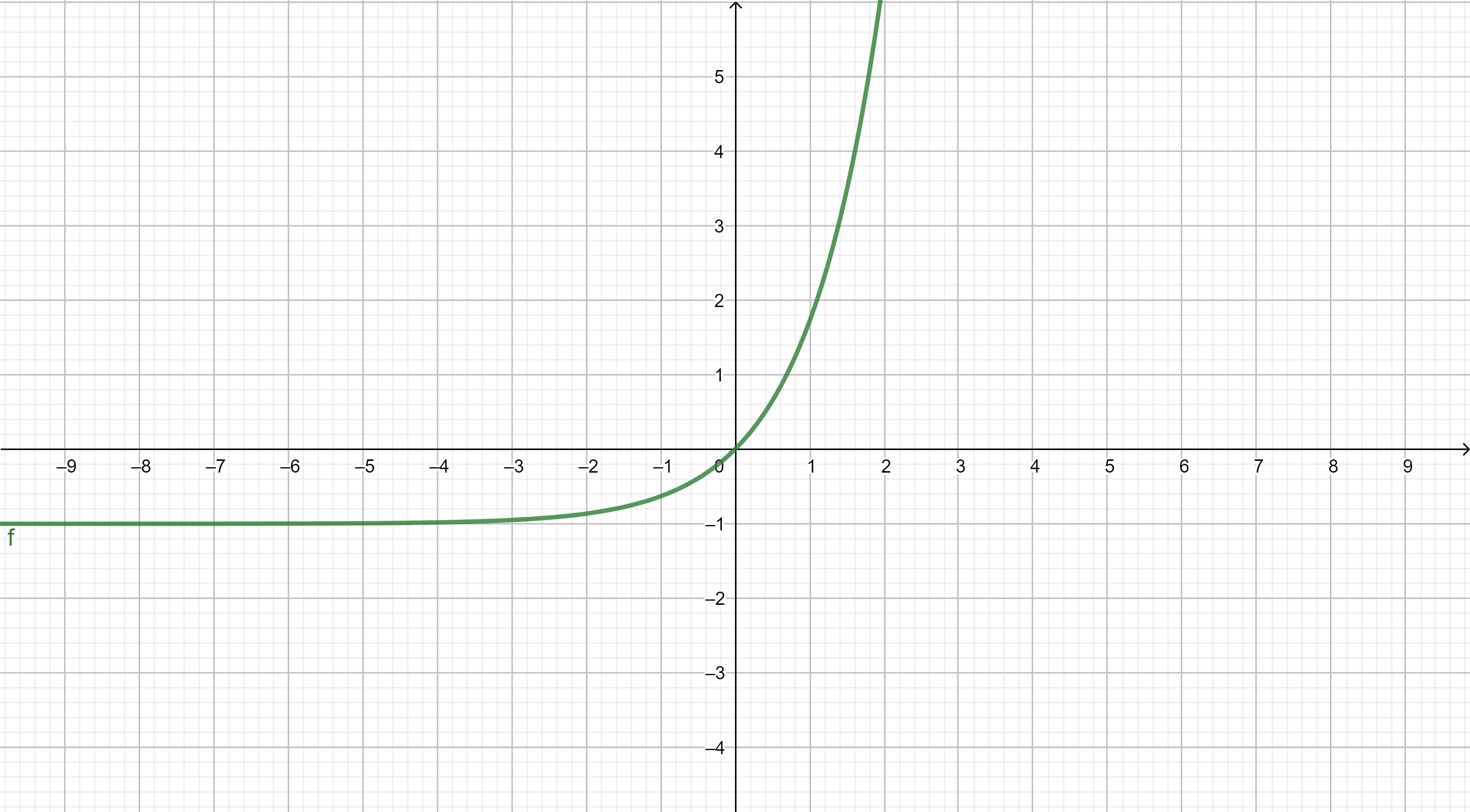
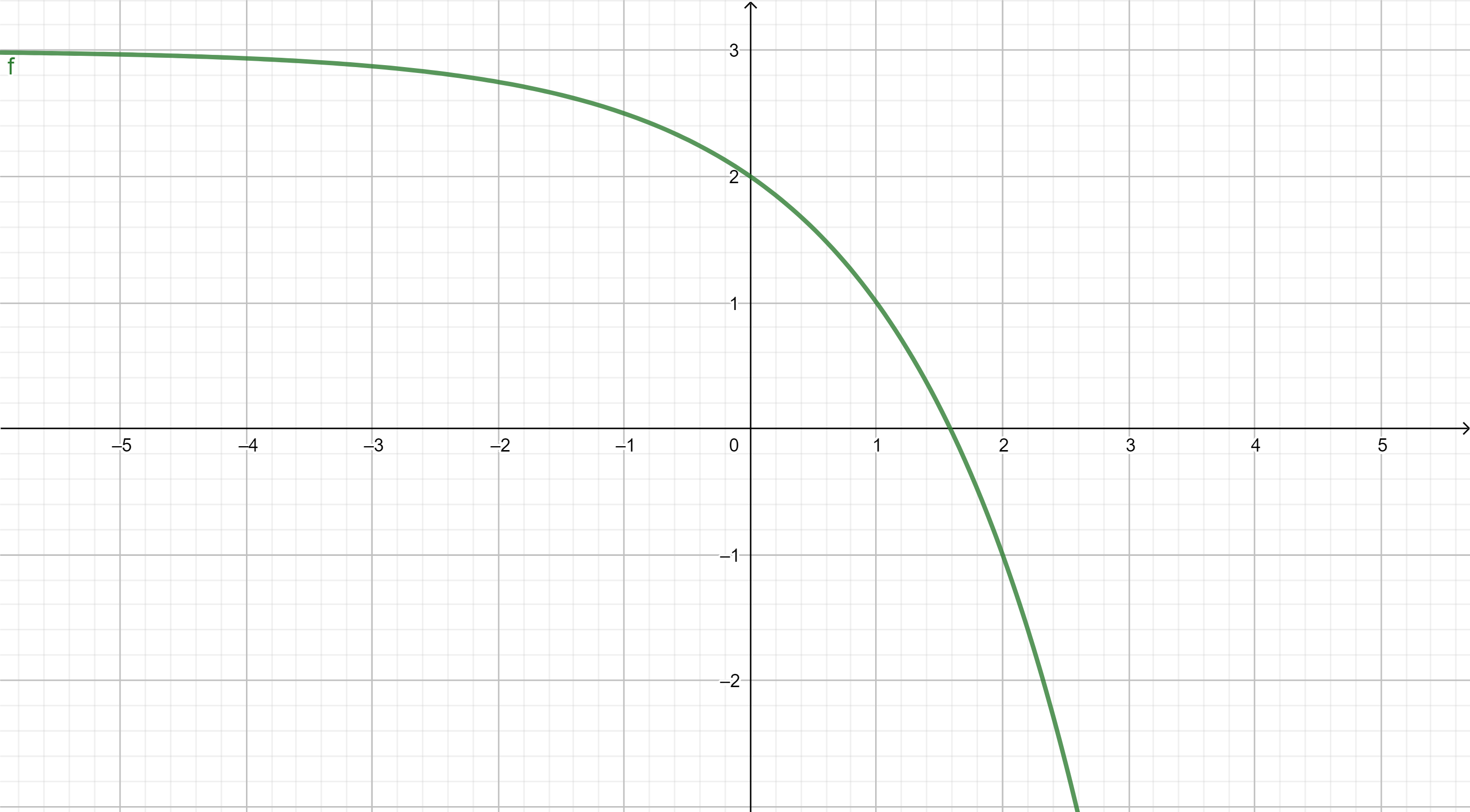
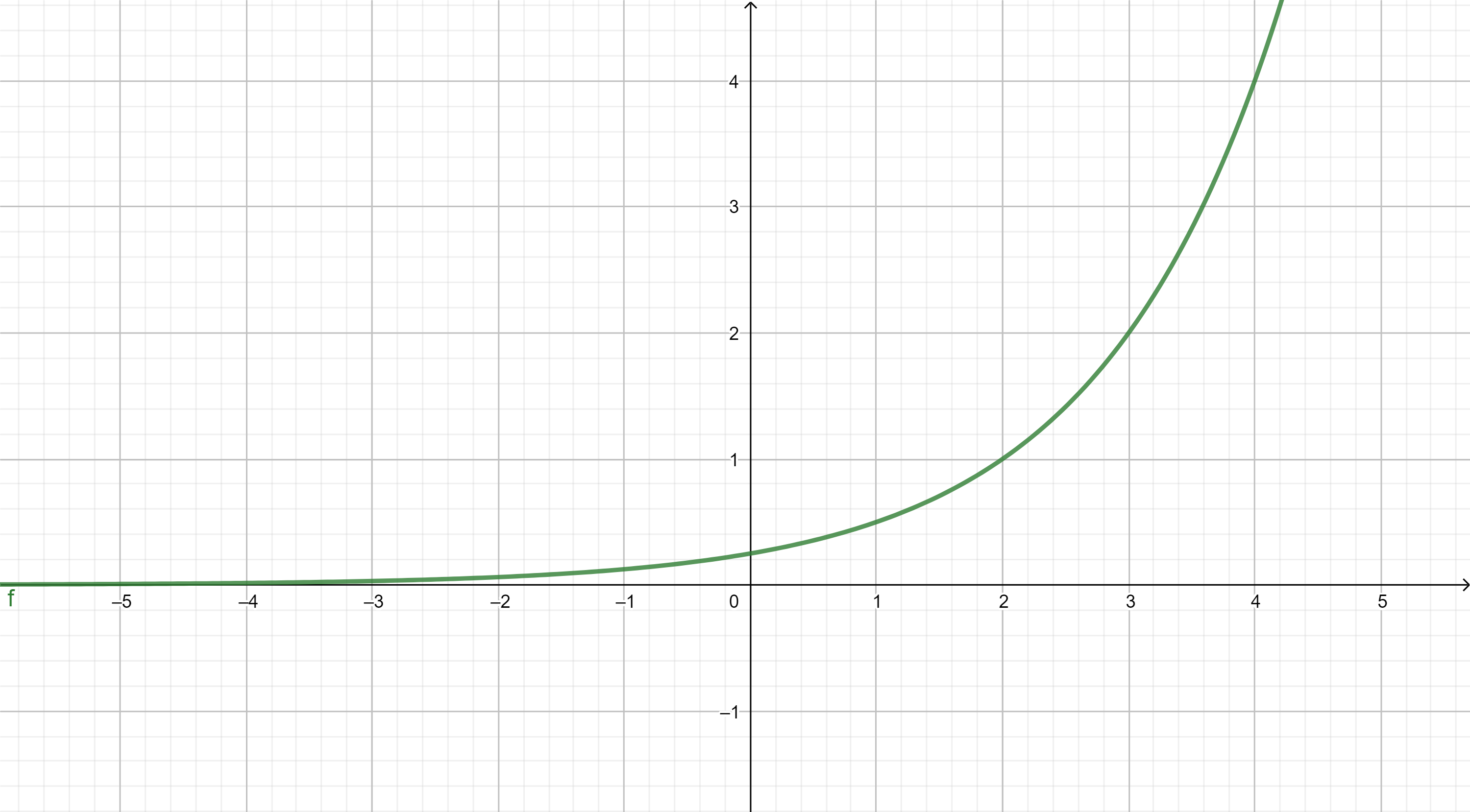
A continuación se muestran, a modo de recordatorio, las gráficas de las funciones elementales. El objetivo es que nos familiaricemos con su "forma" y sus principales propiedades.

  TIPOS DE FUNCIONES ELEMENTALES:

  Identidad

  Cuadrática

  Valor absoluto

  Raíz cuadrada

  Función inversa

  Exponencial

  Logarítmica

  Seno

  Coseno

  Tangente

\(f(x) \rightarrow af(bx+c)+d\)

Sin entrar en mucho detalle:

  • Sumar o restar un número a una función implica "subir" o "bajar" la gráfica de esa función tantas unidades como indique el número.
  • Multiplicar una función por un número positivo mayor que uno contrae la gráfica hacia el eje Y.
  • Multiplicar una función por un número positivo entre cero y uno expande la gráfica.
  • Multiplicar una función por un número negativo "da la vuelta (simetría)" a la gráfica respecto del eje X.
  • Cambiar \(f(x)\) por \(f(x\pm a)\) desplaza la gráfica de la función hacia la izquierdo o derecha.

A continuación se muestran algunos ejemplos de estas transformaciones:

Transf1
Transf2
Transf3
Transf4

  EJERCICIOS.- CARACTERÍSTICAS DE LAS FUNCIONES:

1.- Representa una posible gráfica para una función que cumpla en cada caso las siguientes características:

a)

  • \(Dom(f) = [-4,2) \cap (2, + \infty)\).
  • Máximo local en \((-2,-1)\).
  • Mínimo local en \((0,-3)\).
  • Cortes: \((0,-3), (1,0)\) y \((3,0)\).
  • Asíntota vertical: \(x=2\).
  • Otra tendencia: \(x\to \infty, \ y \to 1\).

b)

  • \(Dom(f) = \mathbb{R}-\left\{0 \right\}\).
  • Es simétrica par.
  • Mínimos en \((-2,0)\) y \((2,0)\).
  • \(x=0\) e \(y=0\) son asíntotas.

c)

  • \(Dom(f)=\mathbb{R}-\left\{1\right\}\).
  • Discontinua en \(x=1\).
  • Máximo en \(x=-1\).
  • Mínimo en \(x=0\).
  • Cortes en \((-3,0), (0,2)\) y \((3,0)\).
  • \(x=1\) e \(y=-1\) son asíntotas.
  • \((1,+\infty)\) la función crece.

2.- Atendiendo a la forma de cada una de las funciones elementales y con ayuda de una tabla de valores, asigna a cada gráfica su función correspondiente.

a) \(f(x) = e^x-1\)

b) \(f(x) = \dfrac{1}{x}+3\)

Texto alternativo de la imagen no establecido
Texto alternativo de la imagen no establecido

c) \(f(x) = \sqrt{x+1}\)

d) \(f(x) = -\ln(2x+4)\)

Texto alternativo de la imagen no establecido
Texto alternativo de la imagen no establecido

e) \(f(x) = \sqrt{-x+1}\)

f) \(f(x) = e^x+3\)

Texto alternativo de la imagen no establecido
Texto alternativo de la imagen no establecido

3.- Atendiendo a la forma de cada una de las funciones elementales y con ayuda de una tabla de valores, asigna a cada gráfica su función correspondiente.

a) \(f(x) = 2-\left|x \right|\)

b) \(f(x) = \log_2(x+2)\)

Texto alternativo de la imagen no establecido
Texto alternativo de la imagen no establecido

c) \(f(x) = -(x-2)^2\)

d) \(f(x) = 2-\log_2(x-3)\)

Texto alternativo de la imagen no establecido
Texto alternativo de la imagen no establecido

e) \(f(x) = \left|x+1 \right|-2\)

f) \(f(x) = 3-2^x\)

Texto alternativo de la imagen no establecido
Texto alternativo de la imagen no establecido

g) \(f(x) = 2^{x-2}\)

h) \(f(x) = 3-(x+1)^2\)

Texto alternativo de la imagen no establecido
Texto alternativo de la imagen no establecido

4.- Calcula el dominio de las siguientes funciones:

a) \(f(x) = \dfrac{x^2-1}{x^2-9}\)

b) \(f(x) = \sqrt{3x+5}\)

c) \(f(x) = \log\left(7x-10 \right)\)

d) \(f(x) = \dfrac{x+3}{x^2+1}\)

e) \(f(x) = \sqrt{1-4x^2}\)

f) \(f(x) = \ln \left(x^2-4x+3 \right)\)

g) \(f(x) = \dfrac{3x-4}{\log_2\left(x^2+3 \right)-2}\)

h) \(f(x) = \dfrac{3x-1}{2x^2-7x+5}\)

i) \(f(x) = \sqrt{x^2+x+2}\)

j) \(f(x) = \dfrac{1-\sqrt{x+1}}{x-5}\)

k) \(f(x) = \dfrac{1-\ln{(7-x)}}{\sqrt{x+3}}\)

l) \(f(x) = \dfrac{x+\ln{x}}{4+5x}\)

Soluciones: 

a) \( \mathbb{R}- \left\{3,-3 \right\} \);     b) \( \left [ -\dfrac{5}{3}, +\infty \right )  \);     c) \( \left (\dfrac{10}{3},+\infty \right ) \);     d) \( \mathbb{R} \);     e) \( \left [\dfrac{-1}{2},\dfrac{1}{2} \right ] \);     f) \(  \left (-\infty, 1 \right )\cup \left ( 3,+\infty \right ) \);     g) \( \mathbb{R}- \left\{1,-1 \right\}  \);     h) \( \mathbb{R}- \left\{1,\dfrac{5}{2} \right\} \);     i) \( \mathbb{R} \);     j) \( \left [ -1, 5 \right )\cup \left ( 5,+\infty \right )   \);     k) \( \left ( -3,7 \right ) \);     l) \( \left ( 0,+\infty \right )  \)

5.- Calcula el dominio de las siguientes funciones:

a) \(f(x) = \dfrac{3}{x-1} + \dfrac{5x}{x+2}\)

b) \(f(x) = \log_2\left(\dfrac{1}{x+7} \right)\)

c) \(f(x) = e^{\frac{1}{x+2}}\)

d) \(f(x) = \ln\left(1+3x+\dfrac{1}{x} \right)\)

e) \(f(x) = \dfrac{\cos x}{2^x-8}\)

f) \(f(x) = \sin \left(\dfrac{3x-1}{x+5} \right)\)

g) \(f(x) = \dfrac{x}{1+\ln\left(2x-3 \right)}\)

h) \(f(x) = \ln \sqrt{\dfrac{x^2}{4-x^2}}\)

i) \(f(x) = \dfrac{x + \ln\left( x-7\right)}{\sqrt{8-x}}\)

Soluciones:

a) \( \mathbb{R}- \left\{1,-2 \right\} \);     b) \( \left (-7, +\infty \right ) \);      c) \( \mathbb{R}- \left\{2 \right\}\);      d) \( \left (0, +\infty \right )\);     e) \(\mathbb{R}- \left\{3 \right\}\);      f) \( \mathbb{R}- \left\{5 \right\}\);      g) \( \left (\dfrac{3}{2}, \dfrac{3+e}{2} \right )\cup \left ( \dfrac{3+e}{2},+\infty \right )\);      h) \( \left (-2, 0 \right )\cup \left ( 0, 2 \right )  \);      i) \( \left (7, 8 \right )\)

Límites y continuidad de una función

Concepto de límite
Límite de una función en un punto

Intuitivamente, es el valor al que se aproxima la función cuando tomamos valores muy próximos al punto. La definición formal de límite en un punto es compleja y en términos matemáticos se escribe como:

\(\displaystyle \lim_{x \to a} f(x) = b \Longleftrightarrow \forall \epsilon > 0, ~ \exists \delta > 0 ~ : \)

\(\displaystyle ~ \left|x-a \right| < \delta \Rightarrow \left|f(x) - b \right| < \epsilon\)

Límite de una función en el infinito

Intuitivamente, es el valor al que se aproxima la función cuando tomamos valores muy grandes de \(x\). La definición formal sería:

\(\displaystyle \lim_{x \to \infty} f(x) = b \Longleftrightarrow \forall \epsilon > 0, ~ \exists M ~ :~ x > M \Rightarrow \left|f(x) - b \right| < \epsilon\)

Límites laterales

Hablamos de límites laterales cuando nos aproximamos al punto solo por uno de los dos lados posibles. Tendremos:

  • Límite lateral por la izquierda: \(\displaystyle \lim_{x\to a^-}f(x)\)
  • Límite lateral por la derecha: \(\displaystyle \lim_{x\to a^+}f(x)\)

En el siguiente vídeo se ilustra el concepto de límite con varios ejemplos.

Video.- Concepto de límite

 CUESTIONARIO.- CONCEPTO DE LÍMITE:

Para la función de la gráfica, calcula \(f(-2): \)
Para la función de la gráfica, calcula \(\displaystyle \lim_{x\to -2^+}: \)
Para la función de la gráfica, calcula \(\displaystyle \lim_{x\to -2^-}:\)
Para la función de la gráfica, calcula \(\displaystyle \lim_{x\to -2}\)

 

 

 

 

Img. cuestionario límite

  EJERCICIOS.- CONCEPTO DE LÍMITE:

1.- Determina el valor de \(f(1), \displaystyle \lim_{x\rightarrow 1^-}f(x), \displaystyle \lim_{x\rightarrow 1^+}f(x) \) y \(\displaystyle \lim_{x\rightarrow 1}f(x)\) en los siguientes casos:

Texto alternativo de la imagen no establecido
Texto alternativo de la imagen no establecido
Texto alternativo de la imagen no establecido

Soluciones:

Soluciones ejer 1 lim

2.- Determina el valor de \(f(2), \displaystyle \lim_{x\rightarrow 2^-}f(x), \displaystyle \lim_{x\rightarrow 2^+}f(x), \displaystyle \lim_{x\rightarrow 2}f(x)\) y de \(f(3), \displaystyle \lim_{x\rightarrow 3^-}f(x), \displaystyle \lim_{x\rightarrow 3^+}f(x)\) y \(\displaystyle \lim_{x\rightarrow 3}f(x)\) en los siguientes casos:

Texto alternativo de la imagen no establecido
Texto alternativo de la imagen no establecido
Texto alternativo de la imagen no establecido
Texto alternativo de la imagen no establecido

Soluciones a y b:

sols 2 ab

Soluciones: c y d:

sols 2 cd

3.- Describe los límites en el infinito \((x\rightarrow \pm\infty)\) de las siguientes funciones:

Texto alternativo de la imagen no establecido
Texto alternativo de la imagen no establecido
Texto alternativo de la imagen no establecido
Texto alternativo de la imagen no establecido

Soluciones:

a) \(\displaystyle \lim_{x\to +\infty} f(x) = +\infty\),  \(\displaystyle \lim_{x\to -\infty} f(x) = +\infty\)

b) \(\displaystyle \lim_{x\to +\infty} f(x) = +\infty\), \(\displaystyle \lim_{x\to -\infty} f(x) = -\infty\)

c) \(\displaystyle \lim_{x\to +\infty} f(x) = 1\), \(\displaystyle \lim_{x\to -\infty} f(x) = -1\)

d) \(\displaystyle \lim_{x\to +\infty} f(x) = 3\), \(\displaystyle \lim_{x\to -\infty} f(x) = -3\)

Continuidad de una función

El concepto de continuidad de una función en un punto, de gran importancia, se define rigurosamente a través de los límites de acuerdo a la siguiente definición.

Diremos que una función \(f(x)\) es continua en un punto \(x=a\) si se cumple:

1.- Existe \(f(a)\)       2.- Existe \(\displaystyle \lim_{x \to a} f(x)\)        3.- \(f(a) = \lim_{x\to a}f(x)\)

Evidentemente, la tercera condición engloba a las otras dos. Cuando tengamos que estudiar si una función es continua en un punto, chequearemos una a una si se cumplen las tres condiciones de la definición anterior.

Una función se dice continua (de forma global) si es continua en todos los puntos donde está definida. Intuitivamente, esto significa que podemos trazar su gráfica sin levantar el lápiz del papel. En el caso de funciones elementales (racionales, irracionales, logarítmicas, exponenciales...etc) para estudiar la continuidad global basta con estudiar el dominio.

Para funciones definidas a trozos hemos de estudiar la continuidad de cada trozo y luego la continuidad en los puntos en los que “terminan o se unen los trozos”.

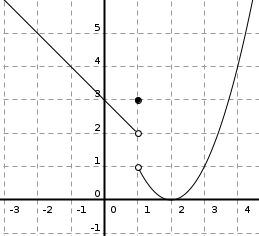
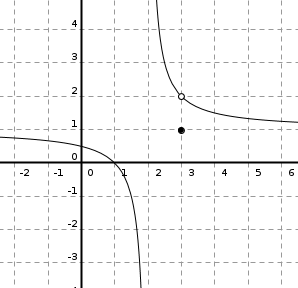
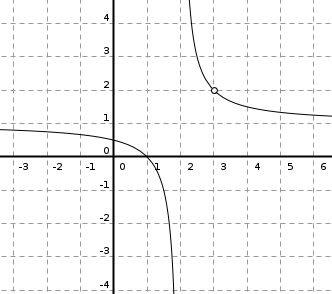
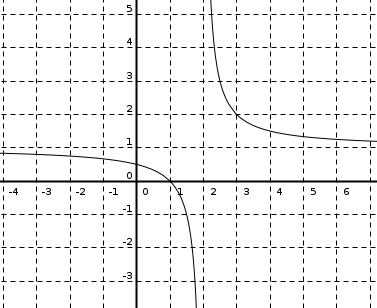
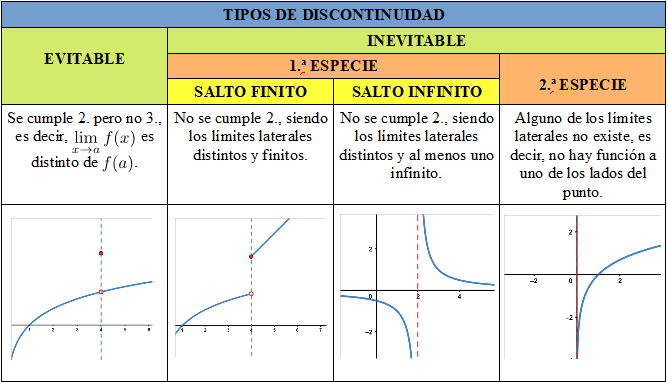
Discontinuidades. Clasificación

Si no se cumple alguna de las condiciones de la definición de continuidad diremos que la función es discontinua en el punto \(x=a\). Según la condición que no se cumpla tendremos un tipo de discontinuidad.

En la tabla de la derecha, se presentan junto a su nomenclatura, los distintos tipos de discontinuidades que podemos tener, haciendo alusión a cuál o cuáles de las condiciones de continuidad (1, 2 o 3) no se cumple.

Texto alternativo de la imagen no establecido

  EJERCICIOS.- CONTINUIDAD DE FUNCIONES

1.- Estudia la continuidad de las siguientes funciones clasificando sus discontinuidades:

a) \(\displaystyle f(x)=\begin{cases}3x+4 & \text{ si } x<-1 \\x^2-4 & \text{ si } x\geq -1 \end{cases} \)

b) \(\displaystyle f(x)=\begin{cases}2-x^2 & \text{ si } x\neq 0 \\0 & \text{ si } x =0 \end{cases} \)

c) \(\displaystyle f(x)=\begin{cases} 4-x & \text{ si } x>3 \\ 1 & \text{ si } -1 < x \leq 3\\ x+2 & \text{ si } x< -1 \end{cases} \)

d) \(\displaystyle f(x)=\begin{cases} \dfrac{1}{x} & \text{ si } x\neq 0 \\ 0 & \text{ si } x =0 \end{cases} \)

2.- Estudia la continuidad de las siguientes funciones según los valores de los parámetros \(a\) y \(b\):

a) \(\displaystyle f(x)=\begin{cases} \left|x^2-4 \right| & \text{ si } x\leq 1 \\ 2x+a & \text{ si } x>1 \end{cases} \)

b) \(\displaystyle f(x)=\begin{cases} \log_2(x^2-5) & \text{ si } x \geq 3 \\ 2^{x+a} & \text{ si } x <3 \end{cases} \)

c) \(\displaystyle f(x)=\begin{cases} a + 2^{x} & \text{ si } x \leq 1 \\ bx+ax^2 & \text{ si } 1< x <3 \\ 1+b+ax & \text{ si } x\geq 3 \end{cases} \)

d) \(\displaystyle f(x)=\begin{cases} 3-kx^2 & \text{ si } x\leq 1 \\ \dfrac{2}{kx} & \text{ si } x>1 \end{cases} \)

e) \(\displaystyle f(x)=\begin{cases} \dfrac{2}{e^x-1}-\dfrac{a}{x} & \text{ si } x \neq 0 \\ -1 & \text{ si } x = 0 \end{cases} \)

f) \(\displaystyle f(x)=\begin{cases} x^2-a & \text{ si } x \leq 1 \\ 2x+a & \text{ si } 1< x <3 \\ b-ax & \text{ si } x\geq 3 \end{cases} \)

3.- La función \(f(x) = \dfrac{x^2-a}{x^3+x^2+ax+12} \) presenta una discontinuidad evitable en \(x=-2\), ¿para qué valor de \(a\)?

4.- Calcula los valores de \(m, n, p\) y \(q\) para que la siguiente función sea continua en todo \mathbb{R}: 

\(f(x)=\left\{\begin{array}{lll}\frac{3}{x} & \text{si} & x < -8\\-2m+3 & \text{si} & -8 \leq x < -4 \\x - \frac{1}{n} & \text{si} & -4 \leq x < 2 \\ px & \text{si} & 2 \leq x \end{array} \right.\)

Teoremas sobre continuidad

Un teorema es un resultado matemático de importancia. Todo teorema se compone de unas hipótesis (condiciones que se tienen que cumplir) y de una tesis (propiedad que se cumple cuando se dan las hipótesis). A continuación se enuncian los tres teoremas más importantes sobre funciones continuas.

  TEOREMAS SOBRE CONTINUIDAD:

Si \(f\) es una función continua en un intervalo \(\left[a, b \right]\) y el signo de \(f(a)\) es distinto del signo de \(f(b)\) entonces existe un \(c \in \left[a,b \right]\) tal que \(f(c) = 0\).

Si \(f\) es una función continua en un intervalo \(\left[a, b \right]\) entonces \(f\) toma todos los valores comprendidos entre \(f(a)\) y \(f(b)\), es decir, para cualquier \(k\) entre \(f(a)\) y \(f(b)\) existe un \(c \in \left[a,b \right]\) tal que \(f(c)=k\).

Si \(f\) es una función continua en un intervalo \(\left[a, b \right]\) entonces \(f\) alcanza un máximo y un mínimo en \(\left[a, b \right]\).

Profundiza: Interpreta y justifica gráficamente el significado de los teoremas sobre continuidad anteriores, de forma que seas capaz de explicarlos con tus propias palabras. Acompaña de una breve reseña histórica sobre dichos teoremas.

Cálculo de límites

Técnicas para el cálculo de límites

Para intentar resolver límites seguiremos siempre los siguientes pasos:

  1. Sustituir el valor al que tiende \(x\) y realizar los cálculos (aquí serán de ayuda las operaciones con límites y con infinitos que veremos a continuación). Si obtenemos un valor real o interpretable ya está.
  2. Si sale una indeterminación, modificaremos el límite de acuerdo al procedimiento oportuno para obtener otro límite equivalente y volver a sustituir. Estos procedimientos también se verán más adelante.

Operaciones con límites

Estas operaciones se pueden utilizar para límites en un punto o en el infinito:

a) \(\lim \left(f\pm g \right)(x) = \lim f(x) \pm \lim g(x)\) 

b) \(\lim \left(f(x) \cdot g(x) \right) = \lim f(x) \cdot \lim g(x)\) 

c) \(\lim \left(\dfrac{f(x)}{g(x)} \right) = \dfrac{\lim f(x)}{\lim g(x)}\)

d) \(\lim \left(k\cdot f(x) \right) = k \cdot \lim f(x)\)

e) \(\lim \sqrt[n]{f(x)} =\sqrt[n]{\lim f(x)}\) (también vale para \(\log_a f(x), \sin f(x)...\))

 f) \(\lim f(x) ^{g(x)} = \lim f(x) ^{\lim g(x)}\)

Operaciones con infinitos

A la hora de manipular infinitos, nos podemos encontrar con las siguientes situaciones:

\(\begin{array}{ccccc}&k\pm\infty=\pm\infty \hspace{2cm} & \ \infty^{k}=\infty~(k>0) \hspace{2cm}& \ k^{\infty}=\infty~(k>1) \hspace{2cm}& \ k^{\infty}=0~(0<k<1)\\&&&&\\&\infty + \infty=+\infty \hspace{2cm}& \ \infty^{k}=0~(k<0)\hspace{2cm}& \ k^{-\infty}=0~(k>1) \hspace{2cm}& \ k^{-\infty}=\infty~(0<k<1) \\ &&&& \\ &\infty\cdot \infty = \infty \hspace{2cm} & \ \dfrac{k}{\infty}=0 \hspace{2cm} & \ 0^{\infty}=0 \hspace{2cm} & \ k\cdot \infty=\infty \\ &&&& \\ & \infty^{+\infty}=+\infty \hspace{2cm} & \ \dfrac{\infty}{k}=\infty \hspace{2cm} & \ \dfrac{a}{0}=\pm\infty~(laterales)&\end{array}\)

 CUESTIONARIO.- OPERACIONES CON INFINITOS:

Calcula: \(\displaystyle \lim_{x\to +\infty} x^2-1000x =\)
Calcula: \(\displaystyle \lim_{x\to -\infty} -2x^4 =\)
Calcula: \(\displaystyle \lim_{x\to +\infty} e^x =\)
Calcula: \(\displaystyle \lim_{x\to -\infty} e^x =\)
Calcula: \(\displaystyle \lim_{x\to +\infty} \left(\dfrac{1}{3} \right)^x =\)
Calcula: \(\displaystyle \lim_{x\to -\infty} 0,5^x =\)

  EJERCICIOS.- CÁLCULO BÁSICO DE LÍMITES:

1.- Halla los siguientes límites aplicando las correspondientes operaciones con infinitos:

a) \(\displaystyle \lim_{x\to \infty}x^{7}\)

b) \(\displaystyle\lim_{x\to -\infty}x^{7}\)

c) \(\displaystyle\lim_{x\to \infty} 7^x\)

d) \(\displaystyle\lim_{x\to -\infty} 7^x\)

e) \(\displaystyle\lim_{x\to \infty} \sqrt[7]{x}\)

f) \(\displaystyle\lim_{x\to -\infty} \sqrt[7]{x}\)

g) \(\displaystyle\lim_{x\to \infty} \left(\sqrt{7} \right)^x\)

h) \(\displaystyle\lim_{x\to -\infty} \left(\sqrt{7} \right)^x\)

i) \(\displaystyle\lim_{x\to \infty} 7^{\frac{1}{x}}\)

j) \(\displaystyle\lim_{x\to -\infty} 7^{\frac{1}{x}}\)

k) \(\displaystyle\lim_{x\to \infty} \left(\frac{1}{7} \right)^x\)

l) \(\displaystyle\lim_{x\to -\infty} \left(\frac{1}{7} \right)^x\)

2.- Halla los siguientes límites aplicando las correspondientes operaciones con infinitos:

a) \(\displaystyle\lim_{x \to 0} 2\)

b) \(\displaystyle\lim_{x\to \infty}x^{-5}\)

c) \(\displaystyle\lim_{x\to -3} \frac{1}{x^2}\)

d) \(\displaystyle\lim_{x\to -\infty}x^{5}\)

e) \(\displaystyle\lim_{x\to -\infty} -7\)

f) \(\displaystyle\lim_{x\to 0^+} \frac{1}{x^{10}}\)

g) \(\displaystyle\lim_{x\to -\infty} \frac{1}{x^{10}}\)

h) \(\displaystyle\lim_{x\to 0^-} \frac{1}{x^{13}}\)

i) \(\displaystyle\lim_{x\to +\infty} \frac{1}{x^{13}}\)

j) \(\displaystyle\lim_{x\to -1} \frac{1}{x^{6}}\)

k) \(\displaystyle\lim_{x\to 0^-} x^3\)

l) \(\displaystyle\lim_{x\to 0^{-}} \frac{1}{x^{6}}\)

3.- Si cuando \(x\to+\infty\) sabemos que \(f(x)\to +\infty\), \(g(x)\to 4\), \(h(x)\to -\infty\) y \(u(x)\to 0\), asigna, cuando sea posible y aplicando las propiedades de las operaciones con límites, el límite cuando \(x\to +\infty\) para cada una de las siguientes expresiones:

a) \(f(x)-h(x)\)

b) \(f(x)^{f(x)}\)

c) \(f(x)+h(x)\)

d) \(f(x)^{x}\)

e) \(f(x)\cdot h(x)\)

f) \(u(x)^{u(x)}\)

g) \(f(x)/h(x)\)

h) \((-h(x))^{h(x)}\)

i) \(g(x)^{h(x)}\)

j) \(u(x)/h(x)\)

k) \(f(x)/u(x)\)

l) \(h(x)/u(x)\)

m) \(g(x)/u(x)\)

n) \(x+f(x)\)

o) \(f(x)^{h(x)}\)

p) \(x+h(x)\)

q) \(h(x)^{h(x)}\)

r) \(x^{-x}\)

s) \(f(x)^2+h(x)^2\)

t) \(f(x)^2-h(x)^2\)

Resolviendo indeterminaciones

Las indeterminaciones en un límite son expresiones en las que no se puede extraer una conclusión inmediata. Para resolver la indeterminación, tendremos que realizar transformaciones en la función del límite que nos permitan obtener una nueva expresión que sí haga posible determinar la solución.

El cálculo de límites se dedica fundamentalmente a las técnicas para resolver estas indeterminaciones.

Las principales indeterminaciones que vamos a encontrar son las siguientes:

\(\left( \dfrac{\infty}{\infty} \right) \ \ \ \left( \dfrac{0}{0}\right) \ \ \ \left( \infty-\infty\right) \ \ \ \left( 0\cdot \infty\right) \ \ \ \left( 1^{\infty}\right) \ \ \ \left( \infty^0\right) \ \ \ \left(0^0\right)\)

  RESOLUCIÓN DE INDETERMINACIONES:

Texto alternativo de la imagen no establecido
Texto alternativo de la imagen no establecido
Texto alternativo de la imagen no establecido
Texto alternativo de la imagen no establecido

Estas indeterminaciones, menos frecuentes, se resolverán tomando logaritmos para transformarlas en otra indeterminación que sí sepamos resolver:

\(\lim f(x)^{g(x)} = e^{\ln \lim f(x)^{g(x)}} = e^{\lim g(x)\cdot \ln f(x)}\)

Texto alternativo de la imagen no establecido

Además de los ejemplos de la tabla anterior, a continuación se proponen algunos límites más que no son demasiado complicados, para que vayas trabajando las técnicas de resolución de indeterminaciones.

También aparecen los links a vídeos donde se resuelven paso a paso los límites.

  • \(\displaystyle \left(\dfrac{k}{0}\right) \rightarrow \lim_{x\to 1}\frac{-2x}{x^2-1}, \ \ \ \ \lim_{x\to 0 } e^{\frac{1}{x}}\)  

Ver soluciones -->  Vídeo

  • \(\displaystyle \left(\dfrac{0}{0}\right) \rightarrow \lim_{x\to 2}\frac{x^2-5x+6}{x^2-4}, \ \ \ \ \lim_{x\to -1}\frac{x+1}{\sqrt{5+x}-2} \) 

 Ver soluciones --> Vídeo

  • \(\displaystyle \left(\dfrac{\infty}{\infty}\right) \rightarrow \lim_{x\to -\infty}\frac{2-3x^2}{2x^2+x-7}, \ \ \ \ \lim_{x\to \infty} \frac{x^2}{x+1} - x \) 
Ver soluciones --> Vídeo
  • \(\displaystyle \left(\infty - \infty\right) \lim_{x\to \infty} \sqrt{x^2-2x}-\sqrt{x+x^2}\) 

Ver soluciones --> Vídeo

  • \(\displaystyle \left(1^{\infty}\right) \rightarrow \lim_{x\to \infty} \left(\frac{x+3}{x} \right)^{x}, \ \ \ \ \lim_{x\to \infty} \left(\frac{x^2+2}{x^2-1} \right)^{x^2+2} \) 

Ver soluciones --> Vídeo

  EJERCICIOS.- CÁLCULO DE LÍMITES:

1.- Resuelve los siguientes límites. Representa gráficamente, de forma local, los resultados obtenidos:

a) \(\displaystyle \lim_{x\to 0} \dfrac{1}{x^2}\)

b) \(\displaystyle \lim_{x\to -1} \dfrac{x+2}{x+1}\)

c) \(\displaystyle \lim_{x\to 0} \dfrac{x^2}{3x\cdot \cos x}\)

d) \(\displaystyle \lim_{x\to 2} \dfrac{1-x}{(x-2)^2}\)

e) \(\displaystyle \lim_{x\to -3} \dfrac{(5-x)^2}{x+3}\)

f) \(\displaystyle \lim_{x\to -3} \dfrac{5-x}{(x+3)^2}\)

Soluciones:

a) \(+\infty\);   b) \(-\infty\) izquierda, \(+\infty\) derecha;   c) \(0\);   d) \(-\infty\);   e) \(-\infty\) izquierda, \(+\infty\) derecha;   f) \(+\infty\) 

2.- Calcula los siguientes límites:

a) \(\displaystyle \lim_{x\to 0} \dfrac{4x}{x^2+3x}\)

b) \(\displaystyle \lim_{x\to 2} \dfrac{2-x}{x^2-2x}\)

c) \(\displaystyle \lim_{x\to -2} \dfrac{x^2-4}{x^2+4x+4}\)

d) \(\displaystyle \lim_{x\to 0} \dfrac{2x^3}{3x\cdot e^x}\)

e) \(\displaystyle \lim_{x\to -1} \dfrac{x^3+1}{-x^2+2x+3}\)

f) \(\displaystyle \lim_{x\to -\sqrt{2}} \dfrac{x^2-2}{x+\sqrt{2}}\)

g) \(\displaystyle \lim_{x\to 0} \dfrac{x^2}{x+x\sin x}\)

h) \(\displaystyle \lim_{x\to 1} \dfrac{x-1}{1-x^2}\)

i) \(\displaystyle \lim_{x\to 0} \dfrac{x\cdot 2^x}{2^x-2^{-x}}\)

Soluciones:

a) 4/3;   b) -1/2;   c) \(+\infty\) izquierda, \(-\infty\) derecha;   d) 0;   e) 3/4;   f)\(-2\sqrt{2}\);   g) 0;   h) -1/2;   i) L'Hôpital \(\dfrac{1}{2\ln 2}\)

3.- Calcula los siguientes límites:

a) \(\displaystyle \lim_{x\to 0} \dfrac{\left| x \right| - 1}{x^2- \left| x\right|}\)

b) \(\displaystyle \lim_{x\to 1} \dfrac{\left| x \right| - 1}{x^2- \left| x\right|}\)

c) \(\displaystyle \lim_{x\to 2} \dfrac{x^2-4}{x-2}\)

d) \(\displaystyle \lim_{x\to -2} \dfrac{x^2-3}{2x+4}\)

e) \(\displaystyle \lim_{x\to -1} \dfrac{\left(1-x \right)^2}{\sin \left( x+1\right)}\)

f) \(\displaystyle \lim_{x\to -3} \dfrac{5-x}{\left( x+3\right)^2}\)

g) \(\displaystyle \lim_{x\to 1} \dfrac{\arctan x}{\ln x}\)

h) \(\displaystyle \lim_{x\to 0^+} \dfrac{\arctan x}{\ln x}\)

i) \(\displaystyle \lim_{x\to 0} \dfrac{\left(e^x+x-1 \right)\cdot \sin x}{\left(e^x+2x-1 \right)\cdot 3x}\)

Soluciones:

a) No entra;   b) No entra;   c) 4;   d) \(-\infty\) izquierda, \(+\infty\) derecha;   e) \(-\infty\) izquierda, \(+\infty\) derecha;   f) \(+\infty\);   g) \(-\infty\) izquierda, \(+\infty\) derecha;   h) 0;   i) L'Hôpital 2/9

4.- Calcula los siguientes límites. Para ello, multiplica por el conjugado de la parte de la fracción que incluya la raíz:

a) \(\displaystyle \lim_{x\to -1} \dfrac{\sqrt{x+2}-1}{x+1}\)

b) \(\displaystyle \lim_{x\to 2} \dfrac{x-2}{\sqrt{x+2}-2}\)

c) \(\displaystyle \lim_{x\to 4} \dfrac{\sqrt{x}-2}{\left| 3-x\right|-1}\)

d) \(\displaystyle \lim_{x\to 1} \dfrac{\sqrt{x}-x}{\left|x-1\right|}\)

e) \(\displaystyle \lim_{x\to 0} \dfrac{\sqrt{e^x}-\sqrt{x+1}}{e^x-1}\)

f) \(\displaystyle \lim_{x\to 1} \dfrac{\sqrt{x}-1}{\sqrt{2-x}-1}\)

g) \(\displaystyle \lim_{x\to -\sqrt{2}} \dfrac{x^2+2}{x+\sqrt{2}}\)

h) \(\displaystyle \lim_{x\to 1} \dfrac{1- x\sqrt{x}}{1-x^2}\)

i) \(\displaystyle \lim_{x\to 2} \dfrac{\sqrt{x+2}-2}{3-\sqrt{x+7}}\)

Soluciones:

a) 1/2;   b) 4;   c) No entra;   d) No entra;   e) L'Hôpital 0;   f) -1 (multiplicar dos veces por el conjugado);   g)  \(-\infty\) izquierda, \(+\infty\) derecha;   h) 3/4;   i) -3/2

5.- Calcula los límites siguientes empleando los órdenes de las funciones involucradas en cada caso:

a) \(\displaystyle \lim_{x\to \infty} x^2 - \sqrt[3]{2x+1}\)

b) \(\displaystyle \lim_{x\to \infty} x^2 - 2^x\)

c) \(\displaystyle \lim_{x\to \infty} 3^x-2^x\)

d) \(\displaystyle \lim_{x\to \infty} 5^x-\sqrt[3]{x^{26}-2}\)

e) \(\displaystyle \lim_{x\to \infty} \sqrt{x}-\log_5 x^4\)

f) \(\displaystyle \lim_{x\to \infty} \dfrac{e^x}{x^2+1}\)

g) \(\displaystyle \lim_{x\to \infty} \dfrac{\ln\left(x^2+x \right)}{3^x}\)

h) \(\displaystyle \lim_{x\to \infty} \dfrac{2^{x-1}}{\sqrt[3]{x^7}}\)

i) \(\displaystyle \lim_{x\to \pi/2} \cos x - \tan x\)

Soluciones:

a) \(+\infty\);   b) \(-infty\);   c) \(+\infty\);   d) \(+\infty\);   e) \(+\infty\);   f) \(+\infty\);   g) 0;   h) \(+\infty\);   i) \(-\infty\) por la izquierda, \(+\infty\) por la derecha.

6.- Halla estos límites:

a) \(\displaystyle \lim_{x \to \infty} \dfrac{x^2+1}{x-2}\)

b) \(\displaystyle \lim_{x \to -\infty} \dfrac{x^2+1}{x-3}\)

c) \(\displaystyle \lim_{x \to \infty} \dfrac{1-x^6}{3x^2+2x-1}\)

d) \(\displaystyle \lim_{x \to -\infty} \dfrac{1-x^6}{3x^2+2x-1}\)

e) \(\displaystyle \lim_{x \to \infty} \dfrac{x^2-2x+3}{x^3-3x^2+5}\)

f) \(\displaystyle \lim_{x \to -\infty} \dfrac{x^2-2x+3}{x^3-3x^2+5}\)

g) \(\displaystyle \lim_{x \to \infty} \dfrac{x^2+1}{3x^2}\)

h) \(\displaystyle \lim_{x \to \infty} \dfrac{1-x^4}{-x^4+2x^2-5}\)

i) \(\displaystyle \lim_{x \to -\infty} \dfrac{16}{x-2}\)

Soluciones:

a) \(+\infty\);   b) \(-\infty\);   c) \(-\infty\);   d) \(-\infty\);   e) 0;   f) 0;   g) 1/3;   h) 1;   i) 0

7.- Calcula los siguientes límites:

a) \(\displaystyle \lim_{x\to \infty} \dfrac{\sqrt{x^2+3}}{2x+1}\)

b) \(\displaystyle \lim_{x\to \infty}\dfrac{2x^2+x-1}{\sqrt{x^2+3}}\)

c) \(\displaystyle \lim_{x\to \infty}\dfrac{2x^2-12x+9}{\sqrt[3]{x^5+5x-2}}\)

d) \(\displaystyle \lim_{x\to \infty}\dfrac{x^2+\sqrt{x}+1}{\sqrt[3]{x^7+1}}\)

Soluciones:

a) 1/2;   b) \(+\infty\);   c) \(+\infty\);   d) 0

8.- Halla estos límites:

a) \(\displaystyle \lim_{x\to \infty} \left( \dfrac{1}{x} - \dfrac{2}{x-1}\right)\)

b) \(\displaystyle \lim_{x\to \infty} \left( \dfrac{x^2+1}{x} - \dfrac{2x^3}{x-1}\right)\)

c) \(\displaystyle \lim_{x\to -\infty} \left( \dfrac{2x^2+3}{5x} + \dfrac{6x-x^2}{3x}\right)\)

d) \(\displaystyle \lim_{x\to \infty} \left( \dfrac{4x^2-1}{5x} \cdot \dfrac{6x}{x^3+1}\right)\)

Soluciones:

a) 0;   b) \(-\infty\);   c) \(-\infty\);   d) 0

9.- Calcula los siguientes límites:

a) \(\displaystyle \lim_{x\to \infty} \sqrt{x+1}-\sqrt{x+2}\)

b) \(\displaystyle \lim_{x\to -\infty} \sqrt{x+1}-\sqrt{x+2}\)

c) \(\displaystyle \lim_{x\to -\infty} \sqrt{x^2+x}-\sqrt{x^2+1}\)

d) \(\displaystyle \lim_{x\to -\infty} x^2-\sqrt{x^4-1}\)

e) \(\displaystyle \lim_{x\to -\infty} 2x-\sqrt{x^2+x}\)

f) \(\displaystyle \lim_{x\to \infty} \sqrt{4x^2-5}-\left(2x-3 \right)\)

g) \(\displaystyle \lim_{x\to \infty} 2x + \sqrt{x^2+x}\)

h) \(\displaystyle \lim_{x\to \infty} x- \sqrt{4x+8}\)

Soluciones:

a) 0;   b) No existe;   c) -1/2;   d) 0;   e) \(-\infty\);   f) 3;   g) \(+\infty\);   h) \(+\infty\)

10.- Estudia los límites en el infinito de las siguientes funciones:

a) \(f(x) = x\cdot \ln\left(\frac{x+1}{x} \right)\)

b) \(g(x) = \left|x+3 \right| - \left|x \right|\)

c) \(h(x)=x\cdot \left(\ln\left(1+x \right)-\ln x \right)\)

d) \(k(x) = x^3+\sin x\)

e) \(a(x) = \dfrac{\ln x \cdot \sqrt{x} \cdot 2^x}{x\cdot e^x}\)

f) \(h(t) = \dfrac{\left|t \right|}{t+1}\)

11.- Calcula:

a) \(\displaystyle \lim_{x\to \infty} \left(\dfrac{x^2+1}{x^2-1} \right)^{x^2}\)

b) \(\displaystyle \lim_{x\to \infty} \left(\dfrac{x-1}{x+3} \right)^{x+2}\)

c) \(\displaystyle \lim_{x\to -\infty} \left(1-\dfrac{1}{x^2} \right)^{3x-2}\)

d) \(\displaystyle \lim_{x\to -\infty} \left(e^x - \dfrac{1}{2x} \right)^{\sqrt{1-x}}\)

e) \(\displaystyle \lim_{x\to \infty} \left(\dfrac{e^{2x}}{e^{x+1}} \right)^{\ln{x}}\)

f) \(\displaystyle \lim_{x\to \infty} \left(\dfrac{2^{x+1}}{e^{x}} \right)^{\sqrt{x^2+1}}\)

g) \(\displaystyle \lim_{x\to \infty} \left(\dfrac{x+1}{x-2} \right)^{2x-1}\)

h) \(\displaystyle \lim_{x\to \infty} \left(\dfrac{5x-2}{5x+3} \right)^{3x}\)

i) \(\displaystyle \lim_{x\to \infty} \left(\dfrac{3x-4}{3x-2} \right)^{\frac{x+1}{3}}\)

j) \(\displaystyle \lim_{x\to \infty} \left(\dfrac{x-3}{x+2} \right)^{x^2-5}\)

k) \(\displaystyle \lim_{x\to \infty} \left(2-\dfrac{x^2+1}{x^2-2} \right)^{\sqrt{2x^2+1}-x}\)

l) \(\displaystyle \lim_{x\to \infty} \left(\dfrac{x^2+1}{x}-\dfrac{x^3-x^2-x+2}{x^2} \right)^{\frac{3-x^2}{x}}\)

12.- Halla los siguientes límites:

a) \(\displaystyle \lim_{x\to \infty} 2^{-x}\cdot x\)

b) \(\displaystyle \lim_{x\to \infty} \left(\dfrac{x^2+3}{x^3-1} \right)\cdot \sqrt{x^3+x}\)

c) \(\displaystyle \lim_{x\to -\infty} \left(\dfrac{2}{x-3} \right)^{\frac{1}{x}}\)

d) \(\displaystyle \lim_{x\to \infty} \left(\dfrac{2}{x-3} \right)^{\sqrt{x}}\)

e) \(\displaystyle \lim_{x\to \infty} x^{\left(\ln \dfrac{x+1}{x} \right)}\)

f) \(\displaystyle \lim_{x\to -\infty} \left( \sqrt{-x}\right)^{e^x }\)

g) \(\displaystyle \lim_{x\to -\infty} \left( \ln\left(1-3x^3 \right)-\ln\left(7-x^3 \right)\right)\)

h) \(\displaystyle \lim_{x\to \infty} x^{1/x}\)

i) \(\displaystyle \lim_{x\to \infty} \dfrac{e^x}{x^3+3}\)

j) \(\displaystyle \lim_{x\to \infty} \dfrac{\ln x^3}{5x-1}\)

k) \(\displaystyle \lim_{x\to -\infty} \dfrac{2^x+4x}{e^x}\)

l) \(\displaystyle \lim_{x\to -\infty} \dfrac{\sqrt{x^2+2x} + x+2}{x+2}\)

m) \(\displaystyle \lim_{x\to -\infty} \left(\dfrac{3x^2+1}{2x^2-2} \right)^{\frac{x-1}{2}}\)

n) \(\displaystyle \lim_{x\to -\infty} \left(\sqrt{x^2-5x}+ x \right)\)

o) \(\displaystyle \lim_{x\to \infty} \left(\dfrac{x+1}{x-2} \right)^{\sqrt{x^2+5x}-x}\)

13.- El número de personas, medido en miles, afectadas por una enfermedad infecciosa según el tiempo transcurrido desde su aparición viene dado por la función:

\( f(x)=\dfrac{90x}{x^2+2x+9} \), donde \(x\) representa el número de días.

a) ¿Cuál es la cantidad inicial de infectados? ¿Y el cuarto día?

b) Estudia el comportamiento de la enfermedad según va avanzando el tiempo. ¿Qué ocurre con la cantidad de infectados cuando el tiempo se hace muy grande?

  Algunas soluciones de los límites paso a paso:

Límites sols 2 y 3
Límites sols 4 y 8
Límites sols 9 y 10

 

Cálculo de asíntotas

Asíntotas

Aunque ya fueron definidas en las características de una función, a continuación se explican las asíntotas a través del concepto de límite, el cual hace más operativo su cálculo.

Vertical

La recta \(x=a\) es una asíntota vertical (A.V) si: 

\(\displaystyle \lim_{x\to a^-} f(x) = \pm \infty\) o \(\displaystyle \lim_{x\to a ^+}f(x) = \pm \infty\).

Texto alternativo de la imagen no establecido

Para su cálculo, tomaremos los valores que no estén en el dominio y veremos si los límites dan infinito. Siempre provienen de la indeterminación \(\left( \dfrac{k}{0}\right)\).

Horizontal en \(+\infty\) (de forma similar en \(-\infty\))

La recta \(y=b\) es asíntota horizontal (A.H) en \(+\infty\) si:

\(\displaystyle \lim_{x \to +\infty} f(x)= b\)

Texto alternativo de la imagen no establecido

La asíntota horizontal en \(-\infty\) se define de forma similar calculando \(\displaystyle \lim_{x\to -\infty} f(x)\).

Oblicua en \(+\infty\) (de forma similar en \(-\infty\))

Solo puede haber asíntotas oblicuas si no hay asíntotas horizontales.

La recta \(y=mx+n\) es asíntota oblicua (A.O) en \(+\infty\) si:

\(\displaystyle m = \lim_{x\to +\infty} \frac{f(x)}{x} \in \mathbb{R}\),

\(\displaystyle n = \lim_{x\to +\infty} \left( f(x) - mx\right)\in \mathbb{R}\)

Texto alternativo de la imagen no establecido

  EJERCICIOS.- CÁLCULO DE ASÍNTOTAS:

1.- Halla, si las hay, las asíntotas verticales y horizontales de las siguientes funciones. Indica también la posición de la función respecto de las asíntotas verticales:

a) \(f(x)=\dfrac{2}{x+1}\)

b) \(f(x)=\dfrac{x+1}{x^2-4}\)

c) \(f(x)=\dfrac{2x}{x-3}\)

d) \(f(x)=\dfrac{-x^2}{(x-1)^2}\)

e) \(f(x)=\dfrac{x^2+2}{x-3}\)

f) \(f(x)=\dfrac{2-x^2}{x}\)

2.- Para las siguientes funciones, determina sus asíntotas oblicuas:

a) \(f(x)=\dfrac{2x^2}{x+1}\)

b) \(f(x)=\dfrac{x^3}{x^2+1}\)

c) \(f(x)=\sqrt{x^2-3x}\)

d) \(f(x)=\sqrt{x^2+x-1}\)

3.- Determina las asíntotas de las siguientes funciones:

a) \(f(x) = \dfrac{2-x}{x^2-4}\)

b) \(f(x) = \dfrac{2-x}{\left(x-3 \right)^2}\)

c) \(f(x) = \dfrac{2-x^2}{x}\)

d) \(f(x) = \sqrt{x^2-1}\)

e) \(f(x) = \sqrt{x^2+2} + \dfrac{1}{x}\)

f) \(f(x) = \dfrac{\sqrt{1-x}}{3x}\)

g) \(f(x) = \dfrac{x+\sqrt{x^2+1}}{x}\)

h) \(f(x) = \dfrac{x}{\ln x}\)

4.- Determina \(A\) y \(B\) para que las rectas \(x=3\) e \(y=\dfrac{3}{4}\) sean asíntotas de la función \(f(x)=\dfrac{Ax+2}{Bx-3}\)

5.- Sabiendo que \(y=2x+6\) es una asíntota oblicua de la función \(f(x) = \dfrac{2x^2+1}{x-k}\), halla el valor del parámetro \(k\).

Derivadas

Concepto de derivada

La derivada es un concepto matemático de enorme importancia, punto de partida de toda una rama de las matemáticas conocida como cálculo diferencial y con incontables aplicaciones en física, química, ingenierías, economía...etc. En esta sección, definiremos la derivada de una función e interpretaremos su significado. Para ello, comenzaremos recordando el concepto de tasa de variación media.

Tasa de variación media (TVM): Dada una función \(f(x)\) en un intervalo \([a,b]\) se define su tasa de variación media como:

\(TVM_{[a,b]} = \dfrac{f(b)-f(a)}{b-a}\)

El concepto de derivada aparece cuando, a la hora de calcular la tasa de variación media, tomamos un intervalo cada vez más pequeño. Es decir, tomamos un intervalo de la forma \([a,a+h]\) y hacemos \(h\) aproximarse a \(0\) \((h\to 0)\).

\(TVM_{[a,a+h]} = \dfrac{f(a+h)-f(a)}{(a+h)-a} = \dfrac{f(a+h)-f(a)}{h} \ \Longrightarrow \ \displaystyle \lim_{h\to 0}\dfrac{f(a+h)-f(a)}{h} \)

Obtenemos entonces la tasa de variación instantánea en el punto \(a\). Esto es precisamente la derivada.

Derivada de una función en un punto: Dada una función \(f(x)\) se define su derivada en el punto \(x=a\) como el siguiente límite, siempre que exista:

\(f^{\prime}(a) = \displaystyle \lim_{h\to 0}\dfrac{f(a+h)-f(a)}{h}\)

Si en la definición anterior llamamos \(x=a+h\) entonces obtenemos otra definición equivalente de derivada:

\(f^{\prime}(a) = \displaystyle \lim_{x\to a}\dfrac{f(x)-f(a)}{x-a}\)

Ejemplo.- Cálculo de la derivada de la función \(f(x) = x^2\) en el punto \(x=2\):

\(f^{\prime}(2) = \displaystyle \lim_{h\to 0}\dfrac{f(2+h)-f(2)}{h} = \displaystyle \lim_{h\to 0}\dfrac{(2+h)^2-2^2}{h} =\)

 \(=\displaystyle \lim_{h\to 0}\dfrac{4+4h+h^2-4}{h} = \displaystyle \lim_{h\to 0}\dfrac{h^2+4h}{h} = \)

\(=\left(\dfrac{0}{0}\right) = \displaystyle \lim_{h\to 0}\dfrac{h(h+4)}{h} =\displaystyle \lim_{h\to 0} h+4 = 4\)

Interpretación geométrica de la derivada

La derivada de una función en un punto se interpreta como la pendiente de la recta tangente a la función en dicho punto. Es decir:

\(f^{\prime}(a) =\) Pendiente de la recta tangente a la curva \(y=f(x)\) en el punto de abscisa \(x=a\)

Ecuación de la recta tangente a \(f(x)\) en el punto \(x=a\): 

                    \(y-f(a) = f^{\prime}(a)(x-a)\)

Vídeo.- Ejemplo recta tangente

Interpretación física de la derivada

Si \(x(t)\) representa la posición de un móvil en función del tiempo la derivada \(x^{\prime}(t)\) representa la variación instantánea de la posición del móvil respecto del tiempo, es decir, la velocidad del móvil en el instante \(t\).

Es habitual en física utilizar la notación de Leibniz para representar la velocidad o la aceleración a través de sus derivadas:

                        \(v(t) = \dfrac{dx(t)}{dt}\)    \(a(t) = \dfrac{dv(t)}{dt}\)

Ejemplo: si un móvil sigue un MRU y su posición en cada instante \(t\) viene dada por la función \(x(t) = 3t + 8\), entonces para obtener su velocidad, tendremos que derivar \(x(t)\) respecto de \(t\).

                        \(v(t) = x^{\prime}(t) = 3\)

Como vemos, la velocidad es constante e igual a 3. La aceleración, al ser la derivada de la velocidad constante, sería 0, lo cual concuerda con el tipo de movimiento.               

Derivadas sucesivas

Llamamos función derivada de \(f(x)\) a la función que asigna a cada \(x\) el valor de la derivada de \(f\) en \(x\). De igual forma, llamamos derivada segunda a la derivada de la función derivada, derivada tercera a la derivada de la derivada segunda… y así sucesivamente:

Esquema de las derivadas sucesivas: $$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \begin{array}{cccc} f^{\prime}: & \mathbb{R} & \longrightarrow & \mathbb{R} \\ & x & \longmapsto & f^{\prime}(x) \end{array} \ \ \ \ \ \ \ \ \ \begin{array}{cccc} f^{\prime\prime}: & \mathbb{R} & \longrightarrow & \mathbb{R} \\ & x & \longmapsto & f^{\prime\prime}(x) \end{array} \ \ \ \ \ \ \ \ \ \begin{array}{cccc} f^{\prime\prime\prime}: & \mathbb{R} & \longrightarrow & \mathbb{R} \\ & x & \longmapsto & f^{\prime\prime\prime}(x) \end{array} \ ...$$
Cálculo de derivadas
Texto alternativo de la imagen no establecido
Texto alternativo de la imagen no establecido

  EJERCICIOS.- DERIVADAS

1.- Empleando la definición, demuestra que \(f(x)\) es derivable en \(x=2\) y determina su derivada en tal punto en los siguientes casos:

a) \(f(x)=x^2\)

b) \(f(x)=\sqrt{x+7}\)

c) \(f(x)=\frac{1}{\sqrt{x-1}}\)

d) \(f(x)=\frac{1}{x+1}\)

e) \(f(x)=\ln(x)\)

f) \(f(x)=5\)

2.- Empleando la definición, calcula la función derivada de \(f(x)\) en los siguientes casos:

a) \(f(x)=x^2\)

b) \(f(x)=\sqrt{x+7}\)

c) \(f(x)=\dfrac{1}{\sqrt{x-1}}\)

d) \(f(x)=\dfrac{1}{x+1}\)

e) \(f(x)=\ln(x)\)

f) \(f(x)=5\)

3.- Demuestra que la función \(f(x)=\sqrt[3]{x}\) no es derivable en \(x=0\).

4.- Calcula la derivada de las siguientes funciones:

a) \(f(x) =x^3+x^2+3\)

b) \(f(x) =4x^5+7x^3-3x+5\)

c) \(f(x) = -3x^4-7x^2-x-1\)

d) \(f(x) =5x^2+7x-6\sqrt[3]{x^4}\)

e) \(f(x) =\sqrt{x}-3x^4\)

f) \(f(x) =\sqrt[3]{x^2}+4\sqrt[5]{x^7}\)

g) \(f(x) =2x^2-\sqrt[3]{x^5}+4\)

h) \(f(x)=\dfrac{7x^5}{3}-8\)

i) \(f(x) =\dfrac{4}{5}x^6-\dfrac{x^5}{3}+\dfrac{x}{4}-\dfrac{1}{2}\)

j) \(f(x) =\dfrac{1}{x^4}-\dfrac{1}{x}\)

k) \(f(x) = \dfrac{2}{x^2}-\dfrac{4}{x}+6\)

l) \(f(x) = \dfrac{x}{\sqrt[3]{x^7}}-\dfrac{4x^6}{5}-3\)

m) \(f(x) = x\cdot\sqrt[3]{x}\)

n) \(f(x) = \dfrac{\sqrt{x^3}\cdot \sqrt[3]{x^4}}{x^2}\)

o) \(f(x)=(2x^2+1)\cdot (\sqrt[4]{x}+x^3)\)

p) \(f(x) =(4x^3-x)\cdot (5x^5-\sqrt[4]{x^7}+1)\)

q) \(f(x) =(\sqrt[4]{x^3}+x)\cdot (3x^6-7\sqrt{x^3})\)

r) \(f(x) = \dfrac{-2x}{7x-3}\)

s) \(f(x) = \dfrac{3-2x}{4x+1}\)

t) \(f(x) = \dfrac{2x^3+5x+3}{x^2+3}\)

u) \(f(x) = \dfrac{x^2+x}{x^3-1}\)

5.- Calcula la derivada de las siguientes funciones:

a) \(f(x) =e^x+\cos x-4x\)

b) \(f(x) =5\sin x-6\cdot e^x+8\sqrt{x}\)

c) \(f(x) = 3\cos x -6\cdot 3^x+8\sin x-x\)

d) \(f(x) =5\sqrt{x} + e^x - 2^x\)

e) \(f(x) =\ln x -3\log x +5x+9\)

f) \(f(x) =7\ln x +\log_2 x +7x-1\)

g) \(f(x) = 3x^5 - \arctan x\)

h) \(f(x)=5\arcsin x - 3\arccos x + 3x-2\)

i) \(f(x)= \ln x - 3\tan x + 5\log_4 x\)

j) \(f(x) =-\arcsin x + 4\arccos x +3x^6-2\)

k) \(f(x) = 4x^5\cdot \ln x\)

l) \(f(x) = \sin x \cdot \cos x\)

m) \(f(x) = 3x^5\cdot e^x\)

n) \(f(x) = (x^3-6x+1)\cdot \sin x\)

o) \(f(x) = (4x^2-x)\cdot \arccos x\)

p) \(f(x) = \arccos x \cdot \arcsin x\)

q) \(f(x) = x\cdot \tan x\)

r) \(f(x) = \ln x \cdot \arctan x\)

s) \(f(x)= \dfrac{e^x}{\cos x}\)

t) \(f(x) =\dfrac{4x^5}{\ln x}\)

u) \(f(x) = \dfrac{\sin x}{\cos x}\)

v) \(f(x) = \dfrac{2x^4+x-4}{\tan x}\)

w) \(f(x) = \dfrac{3x^5}{\arctan x}\)

x) \(f(x) = \dfrac{x^3}{-\sin x}\)

y) \(f(x) = \dfrac{4x^5-3x+1}{\cos x + \sin x}\)

6.- Calcula la derivada de las siguientes funciones:

a) \(f(x) =(3x^4-5x+1)^2\)

b) \(f(x) =(\cos x + 2^x)^5\)

c) \(f(x) = \sqrt{1+2x}\)

d) \(f(x) =\sqrt[3]{(5x+3)^2}\)

e) \(f(x) =\sin^2 x-3x\)

f) \(f(x) =\cos^4 x - 4x^2\)

g) \(f(x) =\cos^2(3x-\dfrac{\pi}{2})\)

h) \(f(x) = \sin(x^2-5x+7)\)

i) \(f(x)= \cos(x^4+3x+1)\)

j) \(f(x)= e^{3x^2-4x}\)

k) \(f(x) = e^{\sin x + 3\cos x}\)

l) \(f(x) = e^{\ln x +\tan x}\)

m) \(f(x) = 7^{x^2-3x+1}\)

n) \(f(x) = 3^{4x^2+4x}\)

o) \(f(x) = \cos(\sqrt{x}-e^x)\)

p) \(f(x) = \tan(5\sqrt{x})\)

q) \(f(x) = -\cos(\sin x -x^2)\)

r) \(f(x) = \sqrt{\cos x + x^3}\)

s) \(f(x)= \sqrt{x^2-2x}\)

t) \(f(x) =\sqrt{\tan(5x)-x}\)

u) \(f(x) = \sqrt[3]{7x^2}\)

v) \(f(x) = -3\sqrt[4]{x^2+\sqrt{x}}\)

w) \(f(x) = \ln(3x^2 + \cos x)\)

x) \(f(x) = \log (e^x+\sin x - x)\)

y) \(f(x) = \ln(\ln x + \tan x)\)

z) \(f(x) = -3 \log_2 (\sqrt{x} + \arctan x)\)

aa) \(f(x) = -7\log_3 (x^4 + \sqrt[5]{x^3})\)

7.- Halla la función derivada utilizando previamente las propiedades de los logaritmos:

a) \(f(x) = \log x^2\)

b) \(f(x) = \log (3x-5)^4\)

c) \(f(x) = \ln(x\cdot \sqrt{x^2+1})\)

d) \(f(x) = \ln \left (\dfrac{3x-1}{4x+5}\right )\)

e) \(f(x) = \log \left(\dfrac{x^5}{1+x^2}\right)\)

f) \(f(x) = \ln\left(\dfrac{x}{2x+5}\right)^{2x-1} \)

8.- Halla la función derivada:

a) \(f(x)=\dfrac{-3}{~\frac{1-x}{1+x}~}\)

b) \(f(x)=\sqrt{\dfrac{1-x}{1+x}}\)

c) \(f(x)=\ln\left(\dfrac{1-x}{1+x}\right)\)

d) \(f(x)=\frac{1-\tan x}{1+\tan x}\)

e) \(f(x)=\sqrt{\frac{1-\tan x}{1+\tan x}}\)

f) \(f(x)=\ln\sqrt{e^{\tan{x}}}\)

g) \(f(x)=\sqrt{3^{x+1}}\)

h) \(f(x)=\log(\sin x\cdot\cos x)^2\)

i) \(f(x)=\dfrac{-3}{\sin^2 x+\cos^2x+x}\)

j) \(f(x)=\sin\sqrt{x+1}\cdot\cos{\sqrt{x-1}}\)

k) \(f(x)=\arcsin\sqrt{x}\)

l) \(f(x)=\sin(3x^5-2\sqrt{x}+\sqrt[5]{2x})\)

m) \(f(x)=\sqrt{\sin x+x^2+1}\)

n) \(f(x) = \cos^2 \sqrt[3]{x+(3-x)^2}\)

o) \(f(x)=\arccos\sqrt{1+x+x^2}\)

p) \(f(x)=\frac{2}{7}\arcsin\left(2^{5x-3}\right)\)

q) \(f(x)=\dfrac{\sin x^3+x^2}{\cos(4x+1)}\)

r) \(f(x)=\dfrac{\sqrt{x^2-1}}{\sqrt{x^2+1}}\)

s) \(f(x) = \dfrac{e^x\cdot \cos x}{2^{x+4}}\)

9.- Halla la ecuación de la recta tangente a las siguientes funciones en el punto indicado:

a) \(y=x^4-2x-3\)    en \(x=-1\)

b) \(y=x^4-2x-3\)    en \(x=0\)

c) \(y=x\ln x\)     en \(x=e\)

d) \(y=\dfrac{x}{x^2+1}\)     en \(x=1\)

10.- Halla las ecuaciones de las rectas tangentes a la curva \(y=\dfrac{x^4}{4}-2x^2+3x\) en los puntos en los puntos en los que su pendiente es 3.

11.- Halla las ecuaciones de las rectas tangentes a la curva \(y=\dfrac{x^3-3x^2}{9}\) en los puntos en los puntos en los que dichas tangentes son paralelas a la bisectriz del primer y tercer cuadrantes.

Nota: la bisectriz del primer cuadrante es la recta \(y=x\) y la del tercer cuadrante \(y=-x\).

Derivabilidad y continuidad

Derivabilidad y continuidad

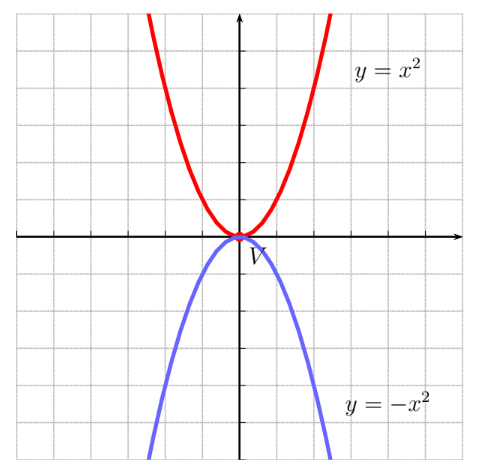
Al igual que existen funciones continuas y discontinuas, existen funciones que son derivables y otras que no. Diremos que una función no es derivable en un punto, o que no tiene derivada, cuando el límite que da la definición de derivada, no exista en dicho punto.

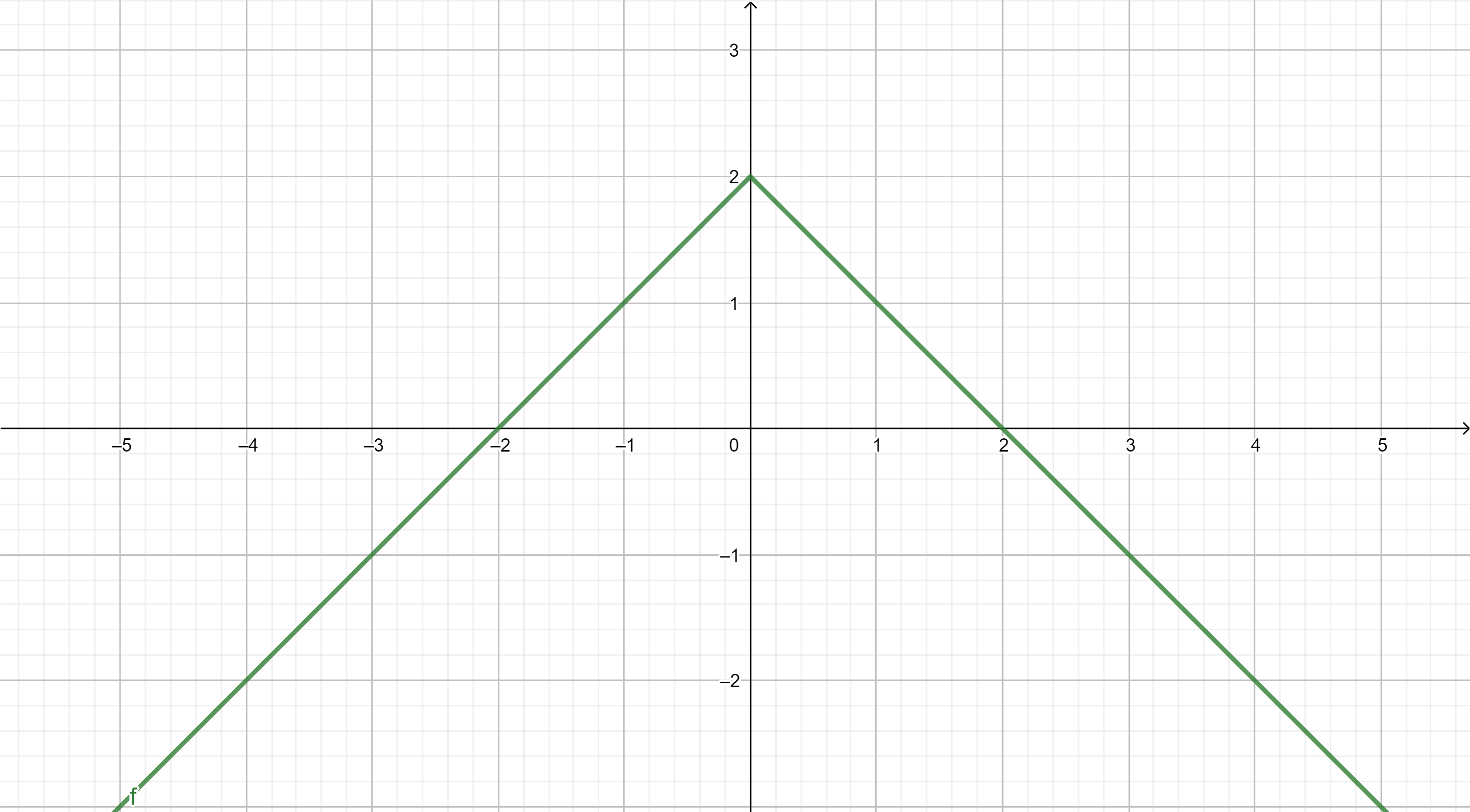
Gráficamente, una función derivable es aquella que no tiene "picos", su gráfica es una curva "suave". Por contra, las funciones que no son derivables en algún punto, presentan un pico en dicho valor.

Analíticamente, una función no será derivable en un punto \(x=a\) cuando no podamos aplicar la definición de derivada, es decir, no exista el límite:

\(\displaystyle \lim_{x\to a}\dfrac{f(x)-f(a)}{x-a}\)

  Función derivable \(f(x)=x^2\)

  Función no derivable \(f(x) = \left | x \right |\)

A la hora de estudiar derivabilidad son útiles las derivadas laterales, que tienen una interpretación muy similar a la de los límites laterales.

Derivada lateral por la izquierda: \(f^{\prime}(a^-) = \displaystyle \lim_{x \to a^-}\dfrac{f(x)-f(a)}{x-a}\)      Derivada lateral por la derecha: \(f^{\prime}(a^+) = \displaystyle \lim_{x \to a^+}\dfrac{f(x)-f(a)}{x-a}\)

Para que una función sea derivable en un punto, han de existir las derivadas laterales en dicho punto y ser iguales.

  EJERCICIOS.- CONTINUIDAD Y DERIVABILIDAD

1.- Estudia la continuidad y derivabilidad de las siguientes funciones a trozos. Halla la función derivada en los puntos donde sea posible:

a) \(f(x)=\left\{\begin{array}{lll} x^2-2x+1 & \text{ si } & x<2\\ -2x+5 & \text{ si } & x\geq 2 \end{array} \right.\)

b) \(f(x)=\left\{ \begin{array}{lll} 2x-5 & \text{ si } & x<3\\ \sqrt{x-2} & \text{ si } & x\geq 3 \end{array} \right.\)

c) \(f(x)=\left\{ \begin{array}{lll} e^x +2 & \text{ si } & x<0\\ x^2+x+3 & \text{ si } & x\geq 0 \end{array} \right.\)

d) \(f(x)=\left\{\begin{array}{lll} \cos x + 2x & \text{ si } & x<0\\ 3x -e^x - 1 & \text{ si } & x\geq 0\\ \end{array} \right.\)

2.- Determina, si es posible, los valores de los parámetros en cada caso para que las siguientes funciones sean derivables en \(\mathbb{R}\):

a) \(f(x)=\left\{\begin{array}{lll} x^2-5x+m & \text{ si } & x\leq 2\\ -x^2+nx & \text{ si } & x> 2 \end{array} \right.\)

b) \(f(x)=\left\{ \begin{array}{lll} mx^2+nx-3 & \text{ si } & x\leq 1\\ 2nx-4 & \text{ si } & x> 1 \end{array} \right.\)

c) \(f(x)=\left\{\begin{array}{lll} (x-1)^3 & \text{ si } & x\leq 0\\ mx+n & \text{ si } & x> 0 \end{array} \right.\)

d) \(f(x)=\left\{ \begin{array}{lll} e^{-x} & \text{ si } & x\leq 0 \\ ax+b & \text{ si } & x> 0 \\ \end{array} \right.\)

e) \(f(x)=\left\{ \begin{array}{lll} x^2+ax-3 & \text{ si } & x\leq 1 \\ \ln (x^2)+b & \text{ si } & x> 1 \\ \end{array} \right.\)

f) \(f(x)=\left\{ \begin{array}{lll} a\sin x+b\cos x & \text{ si } & x<\frac{\pi}{2} \\ \sin^2 x-a\cos x & \text{ si } & x\geq \frac{\pi}{2} \\ \end{array} \right.\)

Soluciones: Apartado a)         Apartado d)           Apartado f)

3.- Considere la función dada por: \(f(x)=\left\{ \begin{array}{lll} \frac{x}{1-e^x} & \text{ si } & x\neq 0 \\ -1 & \text{ si } & x = 0 \\ \end{array} \right. \)

a) Demuestre que la función es continua en todo \(\mathbb{R}\).

b) Determine si la función es derivable en \(x=0\) y, en caso afirmativo, calcule \(f'(0)\).

Solución: Enlace

4.- Estudie la continuidad y derivabilidad de la siguiente función en el punto \(x=0\) y determina su derivada en dicho punto en caso de existir:

\(f(x)=\left\{\begin{array}{lcc}e^{\frac{-1}{x^2}} & \text{ si } & x\neq 0\\ 0 & \text{ si } & x=0 \end{array} \right.\)

5.- Considere la función dada por:  \( f(x)=\left\{\begin{array}{lll} x^2-3x+a & \text{ si } & x\leq 0 \\ -x^2+bx+b+1 & \text{ si } & x> 0 \\ \end{array} \right. \)

Determine los valores de los parámetros \(a\) y \(b\) para que la función sea continua y derivable en todo \(\mathbb{R}\)

Teoremas sobre derivabilidad

Al igual que con las funciones continuas, con las funciones derivables existen una serie de teoremas o propiedades importantes que cumplen este tipo de funciones. Enunciamos a continuación los más importantes, siendo sin duda, la regla de L'Hôpital, por su utilidad práctica, la que más debemos recordar.

  TEOREMAS SOBRE DERIVABILIDAD

Si \(f(x)\) es una función derivable en el punto \(x=a\) entonces también es continua en \(x=a\).

Importante: la afirmación contraria no es cierta en general, es decir, hay funciones continuas en un punto que no son derivables en dicho punto, un ejemplo es la función \(f(x) = \left|x \right|\) que como sabemos es continua en \(\mathbb{R}\) pero no es derivable en ese punto pues tiene “un pico”.

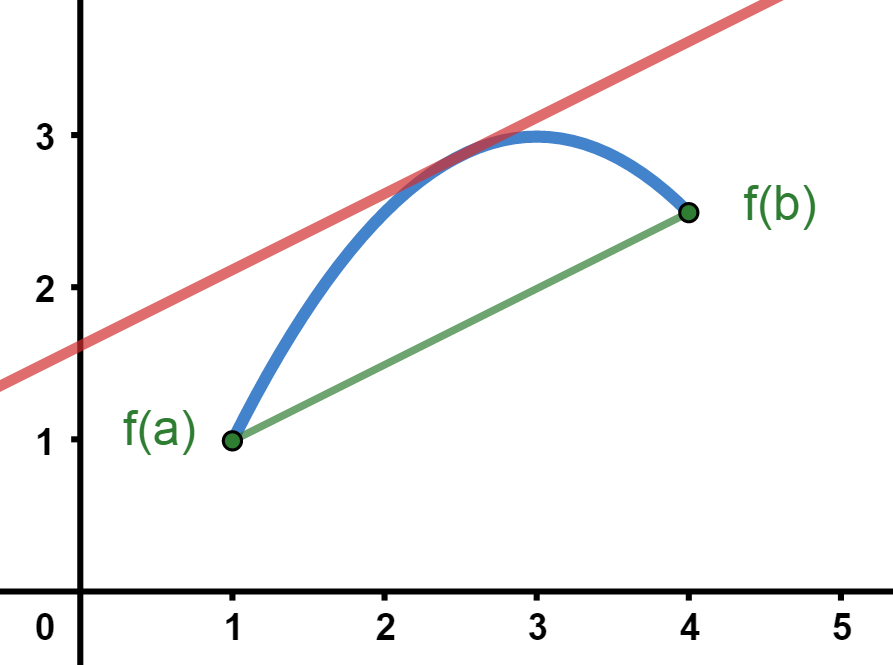
Si \(f: \left[a, b \right] \longrightarrow \mathbb{R}\) es una función que cumple las siguientes hipótesis:

  • Es continua en el intervalo \(\left[a, b \right]\).
  • Es derivable en el intervalo \(\left(a, b \right)\).
  • Toma el mismo valor en los extremos del intervalo \(\left[a, b \right]\), es decir, \(f(a)=f(b)\).

Entonces existe un punto \(c \in \left(a,b \right)\) tal que \(f^{\prime}(c) = 0\), es decir, un punto con tangente horizontal.

Texto alternativo de la imagen no establecido

Si \(f: \left[a, b \right] \longrightarrow \mathbb{R}\) es una función que cumple las siguientes hipótesis:

  • Es continua en el intervalo \(\left[a, b \right]\).
  • Es derivable en el intervalo \(\left(a, b \right)\).

Entonces existe un punto \(c \in \left(a,b \right)\) tal que \(f^{\prime}(c) = \dfrac{f(b) - f(a)}{b-a}\), es decir, un punto con tangente paralela a la cuerda que une \(f(a)\) con \(f(b)\).

Texto alternativo de la imagen no establecido

Para indeterminaciones de la forma \(\left(\dfrac{0}{0} \right)\) y \(\left(\dfrac{\infty}{\infty} \right)\) se tiene que:

\(\displaystyle \lim_{x\to a}\frac{f(x)}{g(x)} = \displaystyle \lim_{x\to a}\frac{f^{\prime}(x)}{g^{\prime}(x)}\)

Siempre que el segundo límite exista.

VIDEO EJEMPLO L`HÔPITAL

Profundiza: busca en internet las demostraciones matemáticas de los teoremas anteriores. Intenta comprenderlas y realiza una pequeña exposición en clase de las mismas.

  EJERCICIOS.- L'HÔPITAL

1.- Calcula los siguientes límites utilizando la regla de L’Hópital:

a) \(\displaystyle\lim_{x\rightarrow 0}\frac{\sin x}{1-\cos x}\)

b) \(\displaystyle\lim_{x\rightarrow 0}\frac{x-\mathrm{sin}x}{x\sin x}\)

c) \(\displaystyle\lim_{x\rightarrow 0}\frac{1-\cos x}{e^x-1}\)

d) \(\displaystyle\lim_{x\rightarrow 0}\dfrac{x-\mathrm{arctan}x}{x-\sin x}\)

e) \(\displaystyle\lim_{x\rightarrow \infty}\frac{\ln x}{x^2+2}\)

f) \(\displaystyle\lim_{x\rightarrow 0}\frac{1-\cos x}{x^2}\)

g) \(\displaystyle\lim_{x\rightarrow -1}\frac{x^2+2x+1}{x^4-1}\)

h) \(\displaystyle\lim_{x\rightarrow 1}\dfrac{1-x^2}{\sin (\pi x)}\)

i) \(\displaystyle\lim_{x\rightarrow 0}\frac{2x^3}{x-\sin x}\)

2.- Calcula los siguientes límites operando primero para obtener las indeterminaciones \(\dfrac{0}{0}\) o \(\dfrac{\infty}{\infty}\) y utilizando después la regla de L’Hópital:

a) \(\displaystyle\lim_{x\rightarrow 0}\left(\frac{1}{x}-\frac{1}{\ln(x+1)}\right)\)

b) \(\displaystyle\lim_{x\rightarrow 0}\left(\frac{1}{e^x-1}-\frac{1}{\sin x}\right)\)

c) \(\displaystyle\lim_{x\rightarrow 0}\left(\dfrac{2}{x^2}-\dfrac{1}{1-\cos x}\right)\)

d) \(\displaystyle\lim_{x\rightarrow 0}\left(\dfrac{1}{x}-\dfrac{1}{\sin x}\right)\)

e) \(\displaystyle\lim_{x\rightarrow 0}\left(\dfrac{1}{x}-\cot x\right)\)

f) \(\displaystyle\lim_{x\rightarrow \infty}\left(\ln(x+1) - \ln x\right)\)

3.- Calcula los siguientes límites tomando primero logaritmos y utilizando la regla de L’Hópital:

a) \(\displaystyle \lim_{x\to 0} (\cos(2x))^{\frac{3}{x^2}}\)

b) \(\displaystyle \lim_{x\to 0} x\ln x\)

c) \(\displaystyle \lim_{x\to 0} (\cot(x))^{\sin(x)}\)

d) \(\displaystyle \lim_{x\to \pi/4} (\tan x -1)\sec(2x)\)

e) \(\displaystyle \lim_{x\to 0} x^{\tan(x)}\)

f) \(\displaystyle \lim_{x\to 0} x^{\sin(x)}\)

  Algunas soluciones.- Límites por L'Hôpital

Solución 1d
Solución eh

Solucion 2c
Solucion 2e

Crecimiento y decrecimiento. Máximos y mínimos

Estudio del crecimiento, decrecimiento y extremos de una función

La primera aplicación de las derivadas que vamos a estudiar es su uso a la hora de determinar el crecimiento, decrecimiento y extremos (máximos y mínimos) de una función. Para ello, hemos de tener en cuenta las siguientes propiedades que cumple la derivada:

  • Crecimiento y decrecimiento:
  1. Si \(f^{\prime}(a)>0\) entonces la función \(f\) es creciente en el punto \(x=a\).
  2. Si \(f^{\prime}(a)<0\) entonces la función \(f\) es decreciente en el punto \(x=a\).
  3. Si \(f^{\prime}(a) =0\) no podemos afirmar nada a priori sobre el crecimiento o decrecimiento de \(f\) en el punto \(x=a\). Decimos que \(x=a\) es un candidato a posible máximo o mínimo.
  • Máximos y mínimos (criterio de la primera derivada):
  1. Si \(f^{\prime}(a)=0\) pero a la izquierda de \(x=a\), \(f^{\prime}(x)>0\) y a la derecha \(f^{\prime}(x)<0\) entonces \(x=a\) es un máximo (relativo) de la función \(f\).
  2. Si \(f^{\prime}(a)=0\) pero a la izquierda de \(x=a\), \(f^{\prime}(x)<0\) y a la derecha \(f^{\prime}(x)>0\) entonces \(x=a\) es un mínimo (relativo) de la función \(f\).
  • Máximos y mínimos (criterio de la segunda derivada):
  1. Si \(f^{\prime}(a)=0\) y \(f^{\prime\prime}(a) <0 \) entonces \(f\) tiene un máximo (relativo) en \(x=a\).
  2. Si \(f^{\prime}(a)=0\) y \(f^{\prime\prime}(a) >0 \) entonces \(f\) tiene un mínimo (relativo) en \(x=a\).
  • Concavidad y convexidad:
  1. Si \(f^{\prime\prime}(a)>0\) entonces \(f\) es convexa en \(x=a\) \((\cup)\).
  2. Si \(f^{\prime\prime}(a)<0\) entonces \(f\) es cóncava en \(x=a\) \((\cap)\).
  3. Si \(f^{\prime}(a)=0\) y \(f^{\prime\prime}(a)=0\) entonces no podemos afirmar nada sobre la concavidad o convexidad de \(f\) y necesitaríamos de herramientas más avanzadas para este estudio. Decimos que \(x=a\) es un punto de inflexión.
Pasos para estudiar el crecimiento de una función

Para estudiar la monotonía de una función \(f(x)\) en general y calcular sus máximos y mínimos, seguiremos los siguientes pasos basados en la teoría anterior:

  1. Calcular el dominio de la función \(Dom ~ f\).
  2. Calcular la derivada de la función \(f^{\prime}(x)\).
  3. Resolver la ecuación \(f^{\prime}(x) = 0\), es decir, buscar los puntos críticos.
  4. Con los puntos críticos y valores que no están en el dominio, formar una tabla y estudiar el signo de la derivada en cada zona.

  EJERCICIOS.- CRECIMIENTO Y DECRECIMIENTO

1.- Determina los intervalos de crecimiento y decrecimiento y los extremos de las siguientes funciones:

a) \(f(x)=\dfrac{\sqrt{x^2-9}}{x-1}\)

b) \(f(x)=\dfrac{x^2}{x-1}\)

c) \(f(x)=\dfrac{e^x}{x}\)

d) \(f(x)=xe^{-x^2}\)

e) \(f(x)=x\ln x -x\)

f) \(f(x)=x\ln x\)

g) \(f(x)=\dfrac{x^2}{e^x}\)

h) \(f(x)=e^\frac{2x}{1+x^2}\)

i) \(f(x)=\dfrac{e^{x-2}+e^{1-x}}{2}\)

2.- Halla los valores de \(a\) y \(b\) en la función \(f(x) = x^2+ax+b \) sabiendo que pasa por el punto \(P(-2,1)\) y que tiene un extremo relativo en el punto de abscisa \(x=-3\).

3.- Halla los valores de los coeficientes de un polinomio de tercer grado \(p(x)\) sabiendo que pasa por el punto \(P(1,0)\), tiene un extremo relativo y que \(p^{\prime}(0)=2 \) y \(p^{\prime}(2)=0 \).

4.- Dada la función \(f(x) = ax + b\sqrt{x} \), determine los valores de los parámetros \(a\) y \(b\) sabiendo que \(f(x)\) cumple las siguientes propiedades:

a) \(f(x)\) alcanza su máximo en el punto de abscisa \(x=100\).

b) La gráfica de \(f(x)\) pasa por el punto de coordenadas \((49,91)\).

5.- Halla \(a\) y \(b\) para que la pendiente de la recta tangente a la función \(f(x) = ax^3+bx\) en el punto \((1,1)\) sea \(-3\).

6.- Halla \(a\) y \(b\) para que la recta tangente a la función \(f(x) = ax^3+bx\) en el punto \((1,1)\) tenga ecuación \(y=x\).

7.- Halla \(a, b, c\) y \(d\) en la función \(f(x) = ax^3+bx^2+cx+d\) sabiendo que el punto \(P(0,4)\) es un máximo y que el punto \(Q(2,0)\) es un mínimo.

Problemas de optimización

Problemas de optimización

Este tipo de problema consiste generalmente maximizar o minimizar una cierta cantidad (es decir, encontrar su máximo o su mínimo) sabiendo que se cumplen ciertas condiciones.

Normalmente, la función inicial tendrá dos variables, \(x\) e \(y\). Tendremos que usar las condiciones que dé el problema para dejarla con una sola variable y después calcular sus máximos o mínimos por el procedimiento habitual.

Ejemplos:

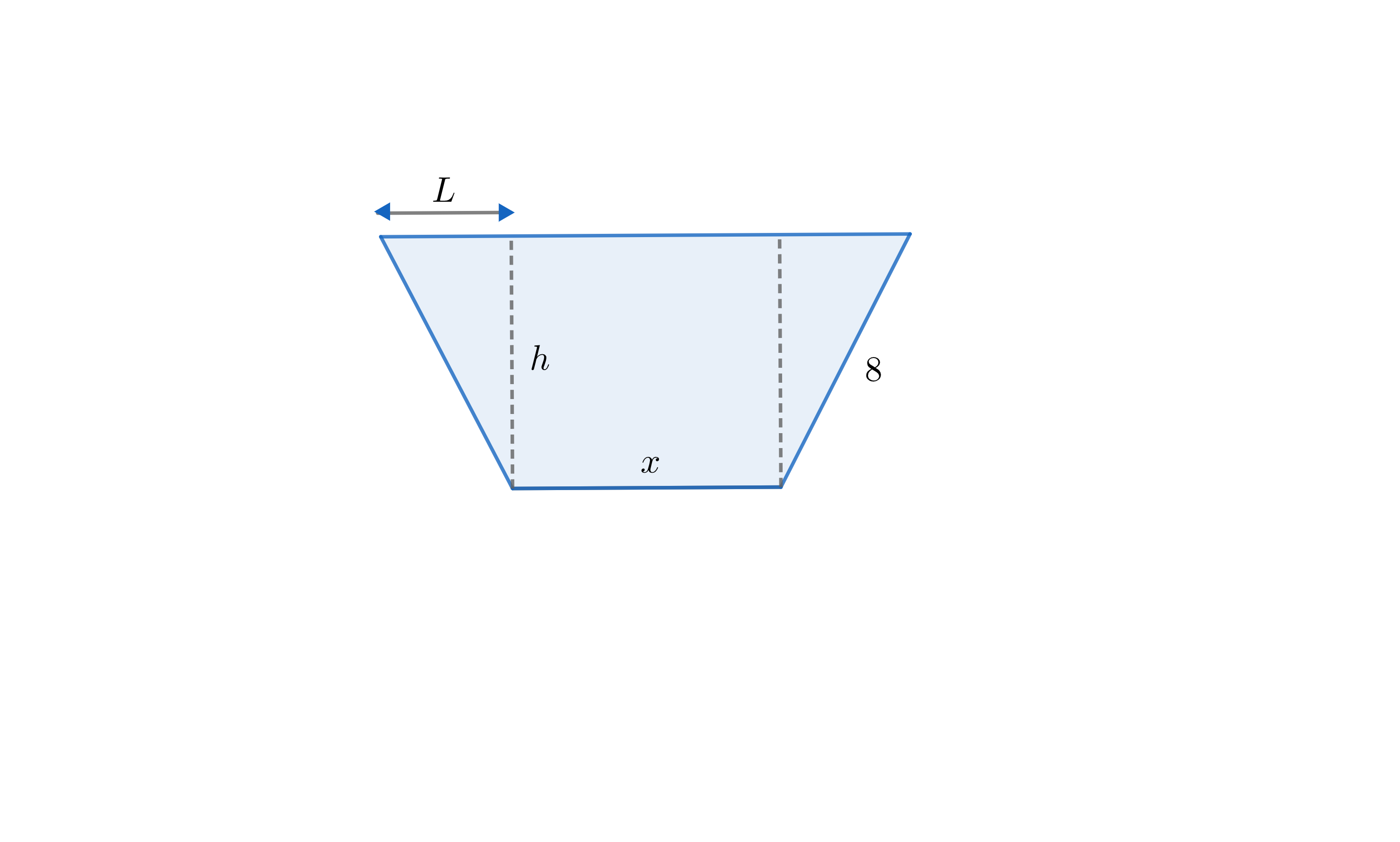
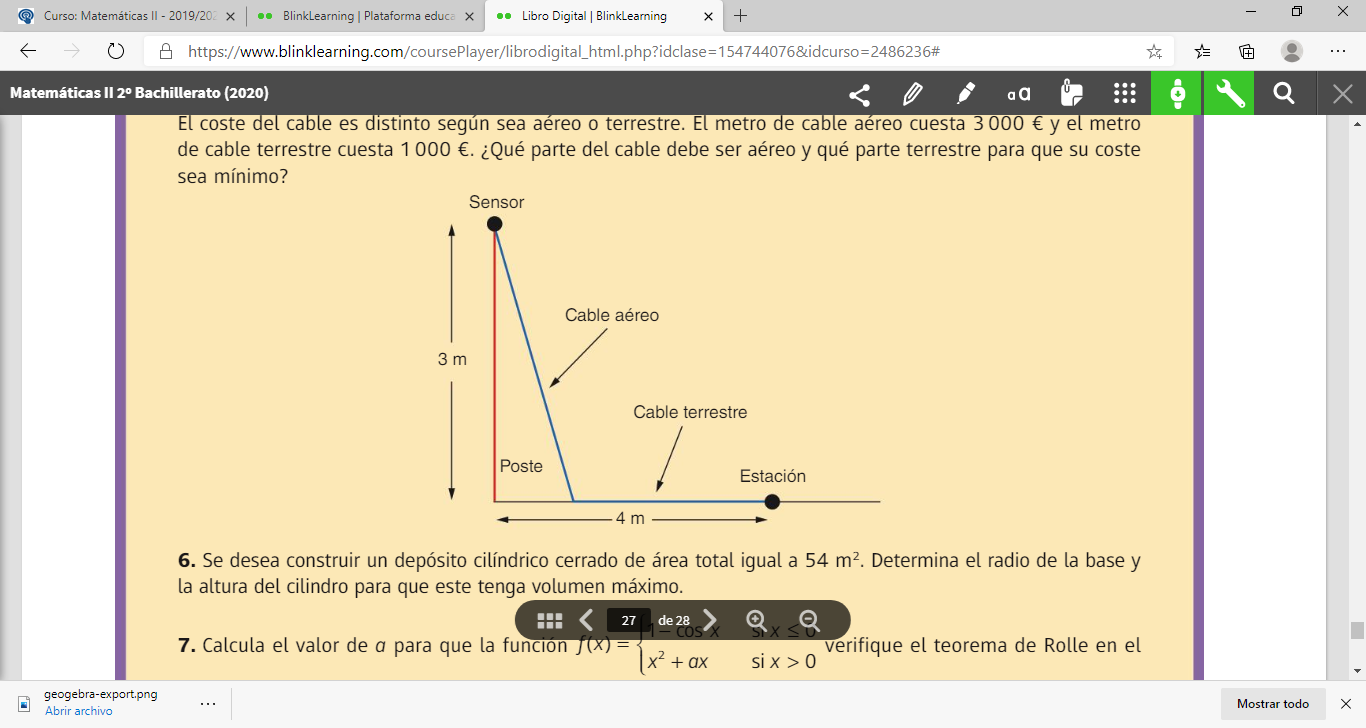
1) Halla dos números positivos cuya suma sea 50 y su producto sea máximo.

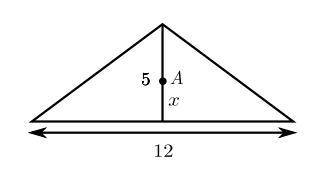
2) Con 100 metros de valla queremos delimitar una zona que sea rectangular. Determina las dimensiones de la parcela para que el área de la misma sea máxima. Determina también dicha área máxima.

3) Una fábrica de latas quiere construir latas cilíndricas cerradas con latón de forma que la superficie total sea de 108 cm². Determina las dimensiones del cilindro (radio de la base y altura) para que el volumen de la lata sea máximo. Halla también dicho volumen máximo.

  EJERCICIOS.- PROBLEMAS DE OPTIMIZACIÓN:

1.- Halla dos números positivos cuya suma sea 100 y su producto sea máximo.

2.- Descomponga el número 48 como suma de dos números positivos de tal manera que el producto de uno de ellos por el cubo del otro sea el mayor valor posible.

3.- Halla tres números no negativos que sumen 14, tales que cada uno sea el doble del otro y la suma de los cuadrados de los tres sea mínima.

4.- Se quiere construir una caja de 2 decímetros de profundidad y con una capacidad de 8 decímetros cúbicos. ¿Qué dimensiones ha de tener para usar la menor cantidad de cartón posible? ¿Qué superficie tendrá la caja en tal caso? (Considera la caja sin tapa).

5.- Determine el radio que ha de tener un recipiente cónico de generatriz 10 cm  para que su volumen sea máximo. Determine dicho volumen.

6.- De todos los triángulos isósceles de perímetro 30 cm, ¿cuál es el de área máxima?

7.- Con una lámina cuadrada de 10 dm de lado se quiere construir una caja sin tapa. Para ello, se recortan unos cuadrados de los vértices. Calcule el lado del cuadrado recortado en cada esquina de la lámina para que el volumen de la caja sea máximo.

8.- Halle las dimensiones que ha de tener un rectángulo inscrito en una circunferencia de radio 1  para que su área sea máxima.

9.- Halle las dimensiones que ha de tener un rectángulo inscrito en una circunferencia de radio \(R\) para que su área sea máxima.

10.- Determine cuáles han de ser las longitudes de los semiejes de una elipse de área \(100\cdot \pi \ cm^2\)   para que su longitud sea mínima.

Indicación: el área y la longitud de una elipse vienen dadas respectivamente por \(A=\pi \cdot ab\) y \(L=\pi\cdot(a+b)\) donde \(a\) y \(b\)  son los semiejes de la elipse.

11.- Halle las dimensiones que ha de tener un cilindro inscrito en una esfera de radio 1 para que su volumen sea máximo.

12.- Un proyectil es lanzado siguiendo una trayectoria parabólica. Si en cada instante (en segundos) la altura del proyectil (en metros) viene dad por la expresión \(h(t)= 42t-t^2\), ¿en qué instante alcanza el proyectil la altura máxima? ¿Cuál es dicha altura máxima? ¿En qué momento cae al suelo?

13.- Calcule el punto de la curva \(y=\frac{1}{1+x^2}\) en el que la pendiente de la recta tangente sea máxima.

14.- De todas las rectas que pasan por el punto \((1,2)\), encuentre la que determina con los ejes de coordenadas, y en el primer cuadrante, un triángulo de área mínima. Calcule el área de dicho triángulo.

15.- Halle el punto de la parábola \(y=x^2\) más cercano al punto \((0,4)\).

16.- Determina los vértices del rectángulo de área máxima cuyos lados son paralelos a los ejes de coordenadas y cuyos vértices están ubicados en los bordes del recinto limitado por las gráficas de las funciones \(f(x)=x^2\) y \(g(x)=2-x^2\).

17.- Un rectángulo tiene sus vértices en los puntos de coordenadas \((0,0), ~ (a, 0), ~ (0,b)\) y \((a,b)\) siendo \(a>0, b>0\) y estando el punto situado en la curva de ecuación:

\(y = \dfrac{1}{x^2}+9\)

De entre todos los rectángulos que cumplen estas condiciones determine el rectángulo de área mínima y calcule su área.

18.- La producción mensual de una fábrica de bombillas viene dada por \(P=2LK^2\)  (en millones), donde \(L\) es el coste de la mano de obra y \(K\) es el coste del equipamiento (en millones de euros). La fábrica pretende producir 8  millones de unidades al mes. ¿Qué valores de \(L\) y \(K\) minimizarían el coste total \(L+K\)?

19.- Considere un triángulo isósceles cuya base de 12 cm es el lado desigual y cuya altura es de 5 cm. Se quiere determinar un punto \(A\) situado sobre la altura a una distancia \(x\) de la base de manera que la suma de las distancias del punto \(A\) a los tres vértices del triángulo sea mínima. Observe la figura de la derecha:

(a) Demuestre que la suma de las distancias del punto \(A\) a los tres vértices del triángulo viene dada por la expresión \(f(x) = 5-x+2\sqrt{x^2+36}\).

(b) Calcule el valor de \(x\) para que la suma de las distancias sea mínima.

(c) Calcule dicha cantidad mínima.

Texto alternativo de la imagen no establecido

20.- Se quiere construir un canal que tenga como sección un trapecio isósceles, de manera que la anchura superior del canal sea el doble de la anchura inferior y que los lados no paralelos sean de 8 metros (observa el esquema del dibujo).

(a) Encuentra el valor del segmento \(L\) del dibujo en función de la variable \(x\) (anchura inferior del canal). Teniendo en cuenta el área de un trapecio, comprueba que, en este caso, el área de la sección viene dada por \(A(x) = \dfrac{3x\sqrt{256-x^2}}{4}\).

(b) Calcula el valor de para que el área de la sección del canal sea máxima.

Texto alternativo de la imagen no establecido

21.- Un poste de 3 m de altura tiene en su punta un sensor que recoge los datos meteorológicos. Dichos datos deben transmitirse a través de una estación de almacenamiento que está situada en el suelo a 4 m de la base del poste. El cable de transmisión puede ser aéreo o terrestre, según vaya por el suelo o el aire.

Si el metro de cable aéreo cuesta 3000 € y el metro de cable terrestre cuesta 1000 €, ¿Qué parte del cable debe ser aéreo y que parte terrestre para que su coste sea mínimo?

Texto alternativo de la imagen no establecido

22.- Las manecillas de un reloj miden 4 y 6 cm; uniendo sus extremos se forma un triángulo.

(a) Demuestre que el área de dicho triángulo viene dada por la función \(A(x)=12\sin x\) donde \(x\) denota el ángulo formado por las manecillas del reloj.

(b) Determine el ángulo que deben formar las manecillas del reloj para que el área de dicho triángulo sea máxima. ¿Cuál es el valor de dicha área máxima? (Se puede utilizar el apartado (a) aunque no se haya demostrado).

23.- Se quiere construir una rampa para camiones de longitud \(L\), con una pendiente \(m=\tan \alpha\) y que salve una altura \(h=20\) metros (siendo \(\alpha\) el ángulo de inclinación de la rampa).

(a) Calcula, en función de \(m\), el valor de la distancia horizontal que abarca la rampa \(b\) y comprueba que la longitud de la rampa puede expresarse como \(L\left(m \right) = 20\sqrt{\dfrac{m^2+1}{m^2}}\).

(b) El camión se mueve a una velocidad constante que depende de la pendiente \(m\) y se expresa en metros por segundo a través de la función \(v(m) = \dfrac{1}{\sqrt{m}}\). Demuestra que el tiempo \(t\), en segundos, que tarda un camión en recorrer la rampa se puede expresar como \(t(m) = 20\sqrt{\dfrac{m^2+1}{m}}\).

(c) Calcula la pendiente \(m\) que hace mínimo el tiempo del recorrido del camión.

Recuerda: Velocidad = Espacio/Tiempo

Vídeos con soluciones:
Más soluciones paso a paso: